MathFun4Kids

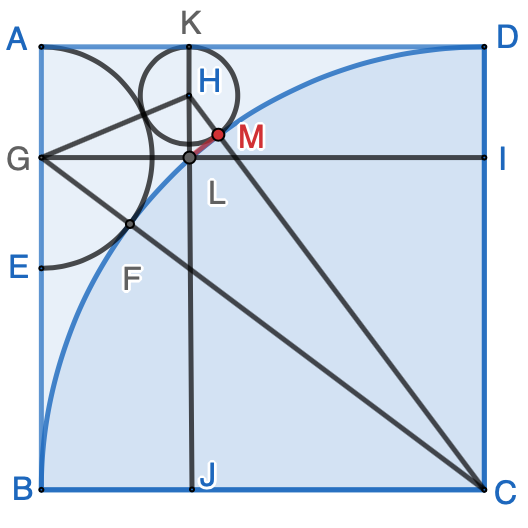
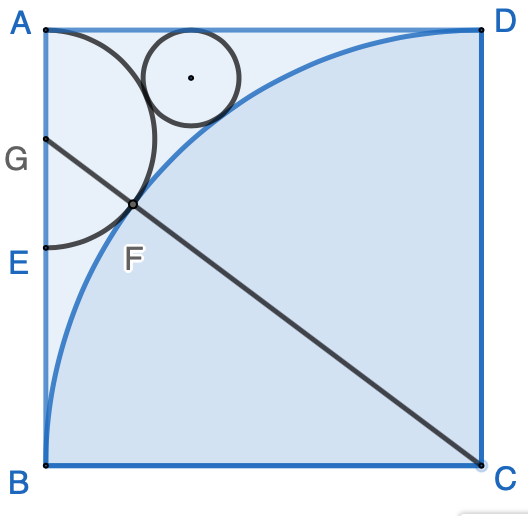
Continue the topic of the previous post in this series, if we construct a semi-circle first, then a quarter circle, and finally a full circle, as the following, what the radius of the full circle?

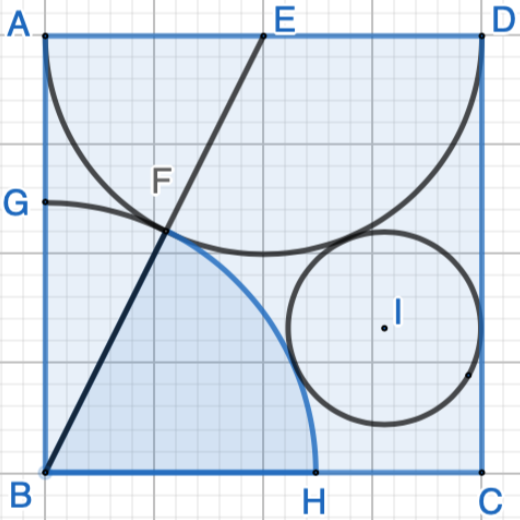
The problem is harder than the previous one, but it is still solvable by following the same steps.

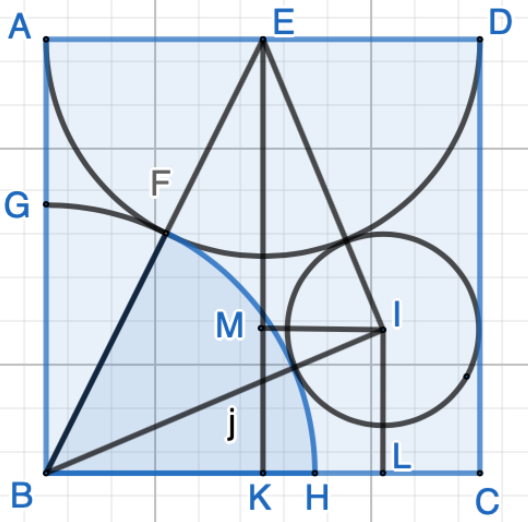
Obviously, the radius of the semi-circle is $\dfrac{1}{2}$. Assume radius of the quarter circle is $q$. According to Pythagoras theorem, $$(\overline{BF}+\overline{EF})^2=\overline{BK}^2+\overline{EK}^2$$ We have $$(q+\dfrac{1}{2})^2=(\dfrac{1}{2})^2+1^2$$ The above equation can be solved as $$q=\dfrac{\pm\sqrt{5}-1}{2}$$ Ignoring the negative $q$ value, we have $$q=\dfrac{\sqrt{5}-1}{2}$$ Let’s denote the radius of the full circle as $r$, and the length of line $\overline{IL}$ and $\overline{MK}$ as $t$. Since $\triangle{BIL}$ and $\triangle{EIM}$ are right triangles, we have $$(q+r)^2 = t^2 + (1-r)^2$$ $$(\dfrac{1}{2}+r)^2=(1-t)^2+(\dfrac{1}{2}-r)^2$$ The above equations can be solved as $$r=\dfrac{3-2\sqrt{2}}{3-\sqrt{5}}, \ \ \ t=\dfrac{2+\sqrt{2}-\sqrt{10}}{3-\sqrt{5}}$$ Simplifying the above values, we have the radius of the full circle as $$ r = \dfrac{9-6\sqrt{2}+3\sqrt{5}-2\sqrt{10}}{4} \approx 0.2245918095$$

To be continued…

Continue the same topic of the previous post in this series, a line is drawn between point L and the tangent point M between the full circle and the quarter circle, as shown in the following figure. Prove $\triangle{HLM}$ is a right triangle.

Based on the result of the previous post, the radius of the full circle is $\dfrac{1}{9}$, the radius of the semi-circle is $\dfrac{1}{4}$, we have: $$\dfrac{\overline{HM}}{\overline{HL}}=\dfrac{\overline{HM}}{\overline{KL}-\overline{HK}}=\dfrac{\dfrac{1}{9}}{\dfrac{1}{4}-\dfrac{1}{9}}=\dfrac{4}{5}$$ $$\dfrac{\overline{HJ}}{\overline{HC}}=\dfrac{\overline{KJ}-\overline{HK}}{\overline{HM}+\overline{MC}}=\dfrac{1-\dfrac{1}{9}}{1+\dfrac{1}{9}}=\dfrac{4}{5}$$ Therefore $$\dfrac{\overline{HM}}{\overline{HL}}=\dfrac{\overline{HJ}}{\overline{HC}}$$ Since $\triangle{HLM}$ and $\triangle{HCJ}$ share the same angle at point $H$, $\triangle{HLM}$ and $\triangle{HCJ}$ are similar. Because $\triangle{HCJ}$ is a right triangle, $\triangle{HLM}$ is also a right triangle.

Can you prove it without calculating the radius of the full circle? To be continued…

Continue the topic in the previous post of this series, we add another circle inscribed in the area bounded by one side of the unit squares, the simi-circle and the quarter-circle, as the following. What is the radius of the circle?

Let’s connect several lines as the following, with line $\overline{GI}$ and $\overline{JK}$ perpendicular to each other and intersecting at point $L$, and point $H$ as the center of the full circle:

Therefore, both $\triangle{GLH}$ and $\triangle{CJH}$ are right triangles. According to Pythagoras theorem, we have: $$\overline{GL}^2+\overline{HL}^2=\overline{GH}^2,\ \ \ \overline{CJ}^2+\overline{HJ}^2=\overline{CH}^2$$ Based on the result of the previous post in this series, the radius of the semi-circle is $\dfrac{1}{4}$. Additionally, since point $C$ is the center of the quarter circle and point $G$ is the center of the semi-circle, both of them are tangent with the full circle centered at point $H$, by assuming the radius of the full circle is $r$ and $\overline{GL} = t$, we have: $$\overline{GH}=\dfrac{1}{4}+r,\ \ \ \overline{HL}=\dfrac{1}{4}-r$$ $$\overline{CH}=1+r, \ \ \ \overline{CJ}=1-t. \ \ \ \overline{HJ}=1-r$$ Therefore, we have the following equations: $$t^2+(\dfrac{1}{4})^2=(\dfrac{1}{4}+r)^2$$ $$(1-t)^2+(1-r)^2=(1+r)^2$$ Simplify the above equations, we have: $$t^2=r, \ \ \ (1-t)^2=4r$$ We have two solutions $$t=\dfrac{1}{3}, \ \ \ r=\dfrac{1}{9}$$ $$t=−1, \ \ \ r=1$$ By ignoring invalid answer $r=1$, we have the answer $r=\dfrac{1}{9}$.

To be continued…

Look at the following figure, a simi-circle is inscribed between the quarter circle and one side of the unit square. What the radius of the semi-circle?

Obviously, $G$ is the center of the semi-circle, line $\overline{CG}$ crosses $F$, the tangent point of the quarter circle and semi-circle, and $\triangle{BCG}$ is a right triangle. According to Pythagoras theorem, we have $$\overline{BC}^2 + \overline{BG}^2 = \overline{CG}^2$$ Assume the radius of the semi-circle is $r$, we have $$\overline{BC}=1$$ $$\overline{BG}=\overline{AB}-\overline{AG}=1-r$$ $$\overline{CG}=\overline{CF}+\overline{GF}=1+r$$ Therefore $$1^2+(1-r)^2=(1+r)^2$$ The above equation can be simplified as $$4r=1$$ Therefore the radius of the semi-circle is $\dfrac{1}{4}$.

Can you solve the problem without using Pythagoras theorem? To be continued…