Look at the following figure, a simi-circle is inscribed between the quarter circle and one side of the unit square. What the radius of the semi-circle?
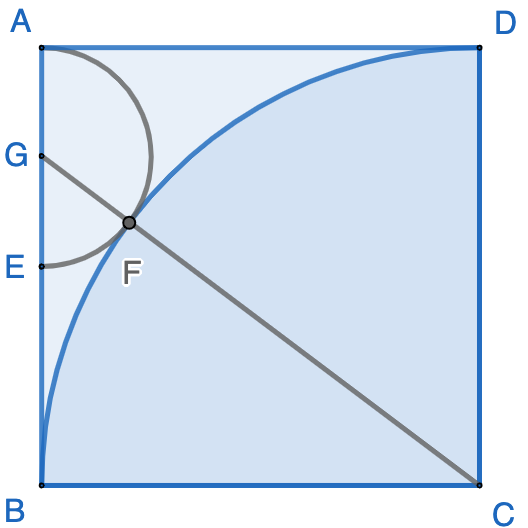
Obviously, $G$ is the center of the semi-circle, line $\overline{CG}$ crosses $F$, the tangent point of the quarter circle and semi-circle, and $\triangle{BCG}$ is a right triangle. According to Pythagoras theorem, we have $$\overline{BC}^2 + \overline{BG}^2 = \overline{CG}^2$$ Assume the radius of the semi-circle is $r$, we have $$\overline{BC}=1$$ $$\overline{BG}=\overline{AB}-\overline{AG}=1-r$$ $$\overline{CG}=\overline{CF}+\overline{GF}=1+r$$ Therefore $$1^2+(1-r)^2=(1+r)^2$$ The above equation can be simplified as $$4r=1$$ Therefore the radius of the semi-circle is $\dfrac{1}{4}$.
Can you solve the problem without using Pythagoras theorem? To be continued…
