Continue the same topic of the previous post in this series, a line is drawn between point L and the tangent point M between the full circle and the quarter circle, as shown in the following figure. Prove $\triangle{HLM}$ is a right triangle.
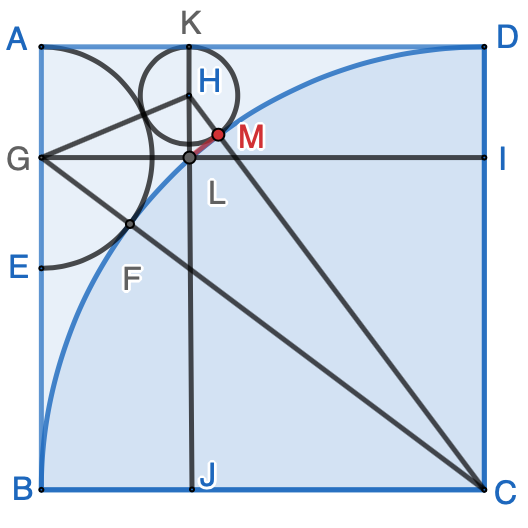
Based on the result of the previous post, the radius of the full circle is $\dfrac{1}{9}$, the radius of the semi-circle is $\dfrac{1}{4}$, we have: $$\dfrac{\overline{HM}}{\overline{HL}}=\dfrac{\overline{HM}}{\overline{KL}-\overline{HK}}=\dfrac{\dfrac{1}{9}}{\dfrac{1}{4}-\dfrac{1}{9}}=\dfrac{4}{5}$$ $$\dfrac{\overline{HJ}}{\overline{HC}}=\dfrac{\overline{KJ}-\overline{HK}}{\overline{HM}+\overline{MC}}=\dfrac{1-\dfrac{1}{9}}{1+\dfrac{1}{9}}=\dfrac{4}{5}$$ Therefore $$\dfrac{\overline{HM}}{\overline{HL}}=\dfrac{\overline{HJ}}{\overline{HC}}$$ Since $\triangle{HLM}$ and $\triangle{HCJ}$ share the same angle at point $H$, $\triangle{HLM}$ and $\triangle{HCJ}$ are similar. Because $\triangle{HCJ}$ is a right triangle, $\triangle{HLM}$ is also a right triangle.
Can you prove it without calculating the radius of the full circle? To be continued…
