Continue the topic in the previous post of this series, we add another circle inscribed in the area bounded by one side of the unit squares, the simi-circle and the quarter-circle, as the following. What is the radius of the circle?
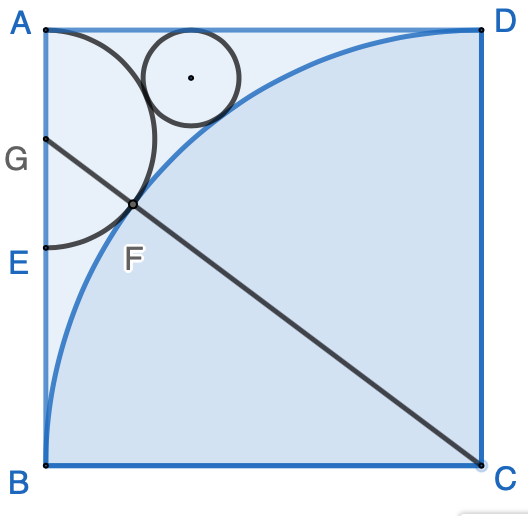
Let’s connect several lines as the following, with line $\overline{GI}$ and $\overline{JK}$ perpendicular to each other and intersecting at point $L$, and point $H$ as the center of the full circle:

Therefore, both $\triangle{GLH}$ and $\triangle{CJH}$ are right triangles. According to Pythagoras theorem, we have: $$\overline{GL}^2+\overline{HL}^2=\overline{GH}^2,\ \ \ \overline{CJ}^2+\overline{HJ}^2=\overline{CH}^2$$ Based on the result of the previous post in this series, the radius of the semi-circle is $\dfrac{1}{4}$. Additionally, since point $C$ is the center of the quarter circle and point $G$ is the center of the semi-circle, both of them are tangent with the full circle centered at point $H$, by assuming the radius of the full circle is $r$ and $\overline{GL} = t$, we have: $$\overline{GH}=\dfrac{1}{4}+r,\ \ \ \overline{HL}=\dfrac{1}{4}-r$$ $$\overline{CH}=1+r, \ \ \ \overline{CJ}=1-t. \ \ \ \overline{HJ}=1-r$$ Therefore, we have the following equations: $$t^2+(\dfrac{1}{4})^2=(\dfrac{1}{4}+r)^2$$ $$(1-t)^2+(1-r)^2=(1+r)^2$$ Simplify the above equations, we have: $$t^2=r, \ \ \ (1-t)^2=4r$$ We have two solutions $$t=\dfrac{1}{3}, \ \ \ r=\dfrac{1}{9}$$ $$t=−1, \ \ \ r=1$$ By ignoring invalid answer $r=1$, we have the answer $r=\dfrac{1}{9}$.
To be continued…
