Problem of the Day – December 5, 2019

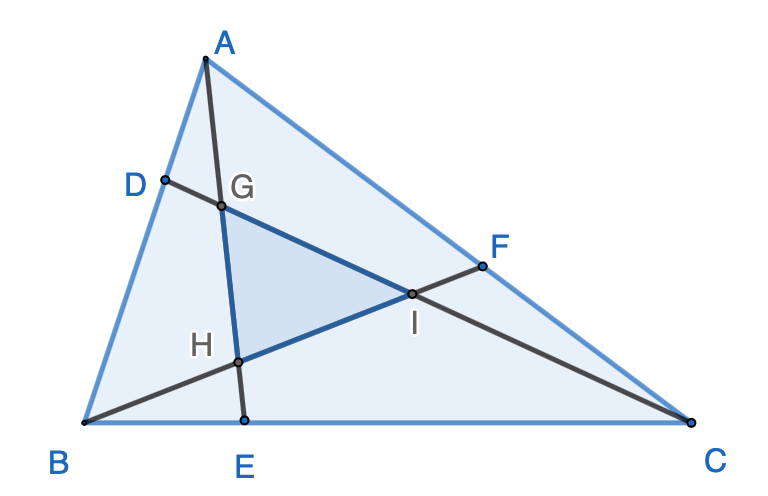
In $\triangle ABC$, $\dfrac{AD}{BD} = \dfrac{1}{2}$, $\dfrac{BE}{EC} = \dfrac{1}{3}$, and $\dfrac{AF}{CF} = \dfrac{3}{2}$. What is the ratio of the area of $\triangle GHI$ to $\triangle ABC$?