MathFun4Kids

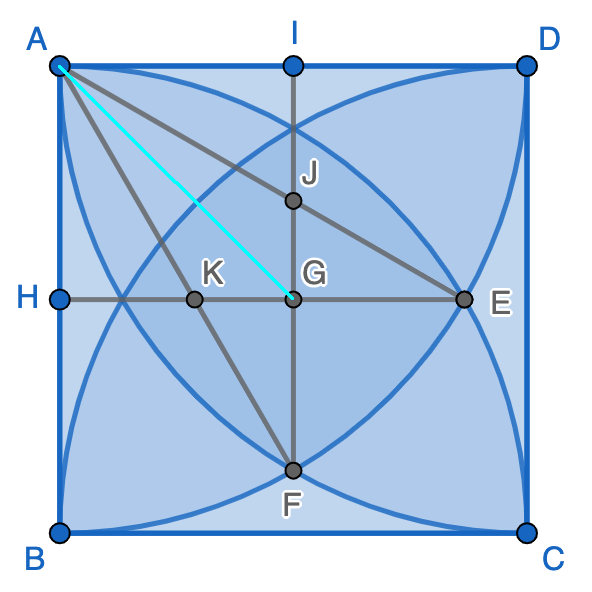
Today, we talk about a classic problem of packing circles in a square. Given a unit square, you need to make 3 congruent, non-overlapping circles that are as big as possible. It has been proven that the arrangement of 3 circles must be as the following. Can you find out what is the radius of the circles?

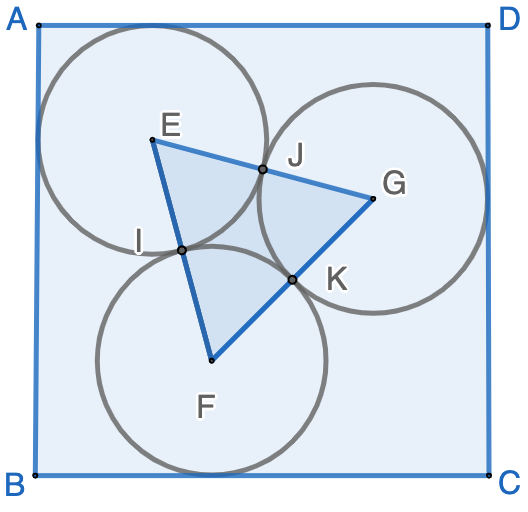
To solve the problem, we can draw various lines as the following so that we can have a clear picture:

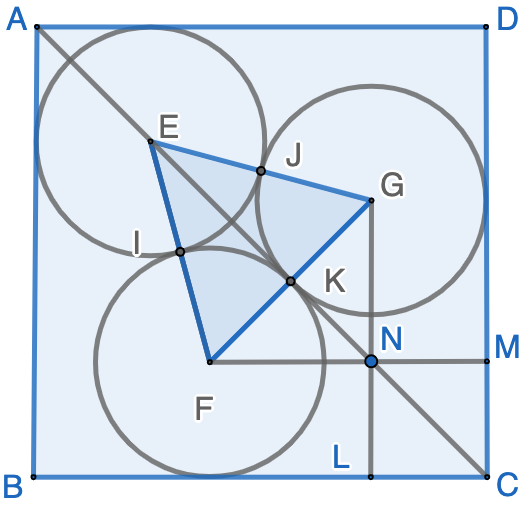
Assume the radius of the circles is $r$. Obviously, $\triangle{EFG}$ is equilateral as $$\overline{EF}=\overline{FG}=\overline{GE}=2\cdot r$$ Therefore, $$\overline{EK}=\dfrac{\sqrt{3}}{2}\cdot\overline{FG}=r\cdot\sqrt{3}$$ Since $$ \overline{AE} + \overline{EK} + \overline{KN} + \overline{NC} = \sqrt{2}$$ we have $$r\cdot\sqrt{2} + r\cdot\sqrt{3} + r + r\cdot\sqrt{2}=\sqrt{2}$$ Therefore $$r=\frac{\sqrt{2}}{1 + 2\sqrt{2}+\sqrt{3}}=\frac{2}{4+\sqrt{2}+\sqrt{6}}$$ $$ = \frac{1}{2}(8-5\sqrt{2}+4\sqrt{3}-3\sqrt{6}) \approx 0.2543331$$

Additional information about circle packing in a square can be found at here or here.

In the previous post of this series, we asked if the area of the region can be solved without using previous calculation. Look at the figure below, after drawing several lines by connecting several points:

The fan area of $[AEF]$ is $\dfrac{\pi}{12}$, because line $\overline{AE}$ and $\overline{AF}$ trisect the right angle at $A$.

Additionally,

$$\overline{EG}=\overline{FG}=\overline{EH}-\overline{GH}=\dfrac{\sqrt{3}}{2}−\dfrac{1}{2}=\dfrac{\sqrt{3}-1}{2}$$ $$[\triangle{AGE}]=[\triangle{AGF}]=\dfrac{1}{2}\cdot\overline{EG}\cdot\overline{AH}=\dfrac{1}{2}\cdot\dfrac{\sqrt{3}-1}{2}\cdot\dfrac{1}{2}=\dfrac{\sqrt{3}-1}{8}$$ $$[GEF]=[AEF]-[\triangle{AGE}]-[\triangle{AGF}]=\dfrac{\pi}{12}-2\cdot\dfrac{\sqrt{3}-1}{8}=\dfrac{1}{4}-\dfrac{\sqrt{3}}{4}+\dfrac{\pi}{12}$$

The area of the middle region bounded by the four quarter circles is:

$$ 4\cdot [GEF]=4\cdot(\dfrac{1}{4}-\dfrac{\sqrt{3}}{4}+\dfrac{\pi}{12})=1-\sqrt{3}+\dfrac{\pi}{3}$$

The above shows the same answer as given in the previous post. To be continued…