In the previous post of this series, we asked if the area of the region can be solved without using previous calculation. Look at the figure below, after drawing several lines by connecting several points:
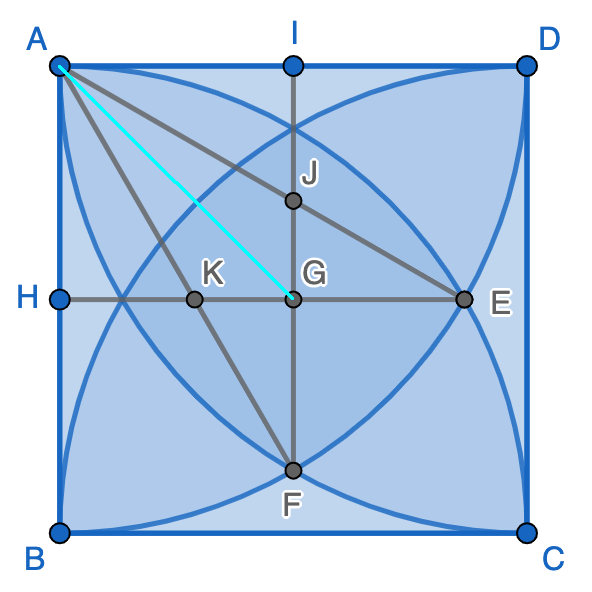
The fan area of $[AEF]$ is $\dfrac{\pi}{12}$, because line $\overline{AE}$ and $\overline{AF}$ trisect the right angle at $A$.
Additionally,
$$\overline{EG}=\overline{FG}=\overline{EH}-\overline{GH}=\dfrac{\sqrt{3}}{2}−\dfrac{1}{2}=\dfrac{\sqrt{3}-1}{2}$$ $$[\triangle{AGE}]=[\triangle{AGF}]=\dfrac{1}{2}\cdot\overline{EG}\cdot\overline{AH}=\dfrac{1}{2}\cdot\dfrac{\sqrt{3}-1}{2}\cdot\dfrac{1}{2}=\dfrac{\sqrt{3}-1}{8}$$ $$[GEF]=[AEF]-[\triangle{AGE}]-[\triangle{AGF}]=\dfrac{\pi}{12}-2\cdot\dfrac{\sqrt{3}-1}{8}=\dfrac{1}{4}-\dfrac{\sqrt{3}}{4}+\dfrac{\pi}{12}$$The area of the middle region bounded by the four quarter circles is:
$$ 4\cdot [GEF]=4\cdot(\dfrac{1}{4}-\dfrac{\sqrt{3}}{4}+\dfrac{\pi}{12})=1-\sqrt{3}+\dfrac{\pi}{3}$$The above shows the same answer as given in the previous post. To be continued…
