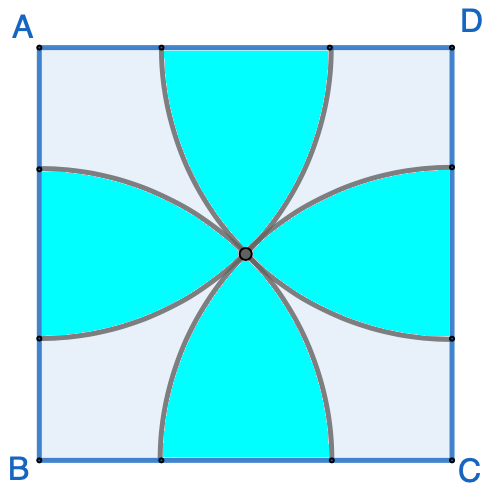
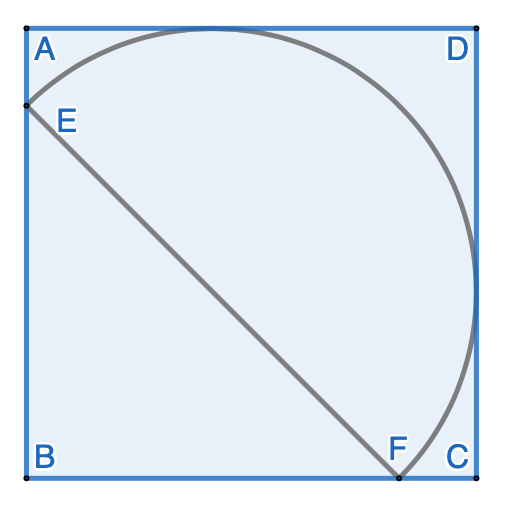
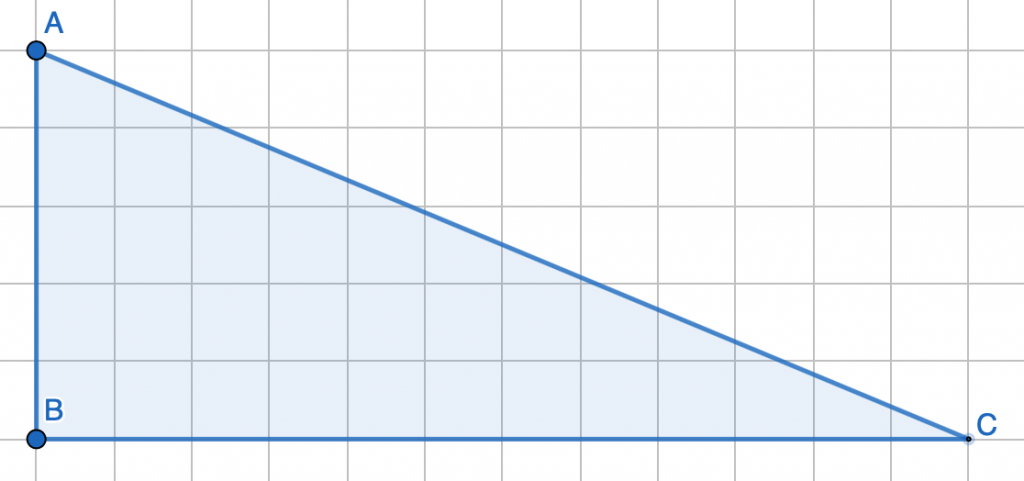
By connecting various points in the figure, we have the following:
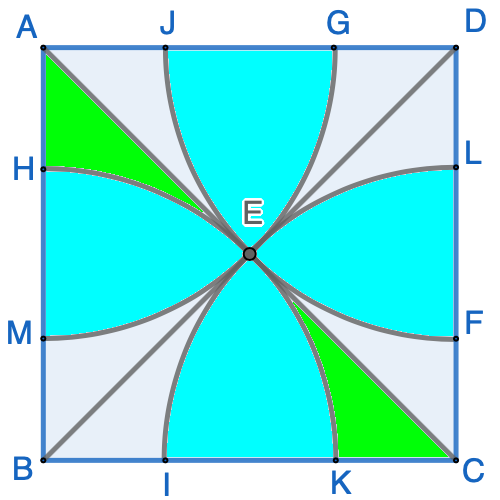
It is obvious that the radius of each quarter circle is $\dfrac{\sqrt{2}}{2}$, and the area of two green regions is: $$\dfrac{1}{2}-\dfrac{1}{4}\cdot\pi\cdot(\dfrac{\sqrt{2}}{2})^2=\dfrac{1}{2}-\dfrac{\pi}{8}$$ Therefore, the total area of the blue regions is equal to the area of the unit square minus 4 times of the area of the two green regions: $$1-4\cdot(\dfrac{1}{2}-\dfrac{\pi}{8})=\dfrac{\pi}{2}-1$$
In the following figures, 4 quarter circles join at the center of a unit square. Find the area of the shaded regions in blue.
In the following figure, a semi-circle is inscribed with maximum size inside a unit square. Find the radius of the the semi-circle.
According to Pythagoras theorem, the length of the street is $13$ blocks. However, if you look at the following diagram, Bob actually walks 16 street blocks 🙂
Bob walks to school by walking up Geometry Street for 5 blocks, and turning 90 degrees to the right onto Square Street for 12 blocks. There is also a street that runs directly from Bob’s house to his school. If Bob walks along this street, how many blocks will he walk?
