MathFun4Kids

MATHCOUNTS Exercise – 22

Posted on January 1, 2021 by kevin

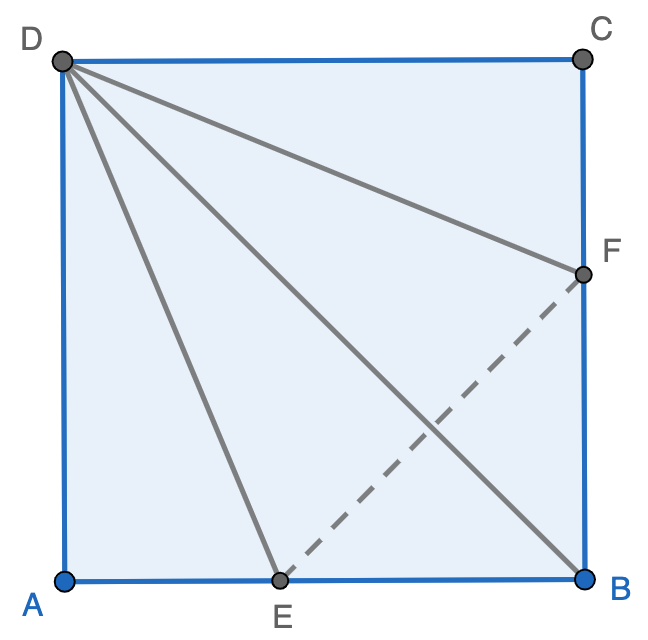
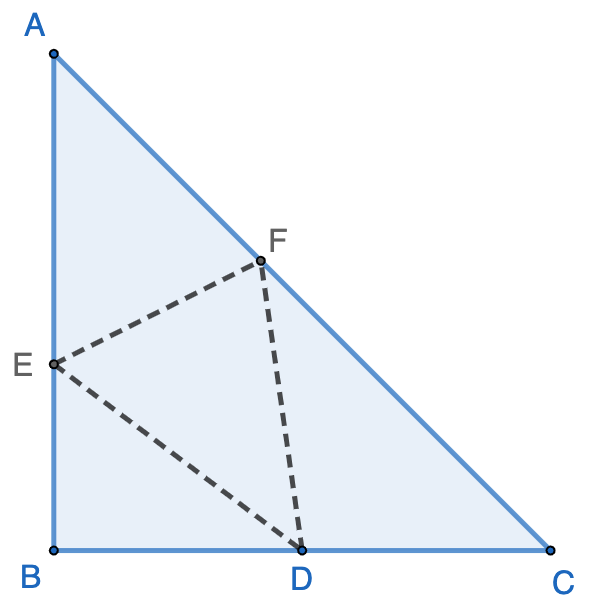
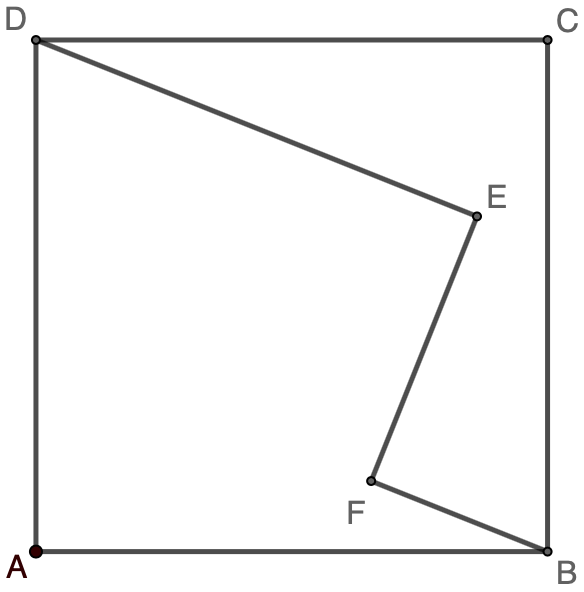
Point $E$ and $F$ are inside the square $ABCD$, with $DE=10$, $EF=6$, $BF=4$, and $\angle{DEF}=\angle{BFE}=90^\circ$. Find the area of the square $ABCD$. Click here for the solutions.

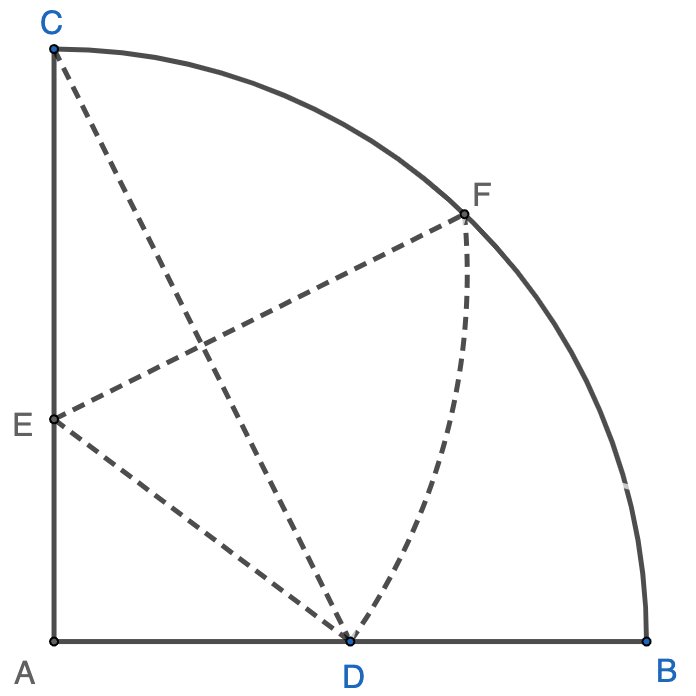
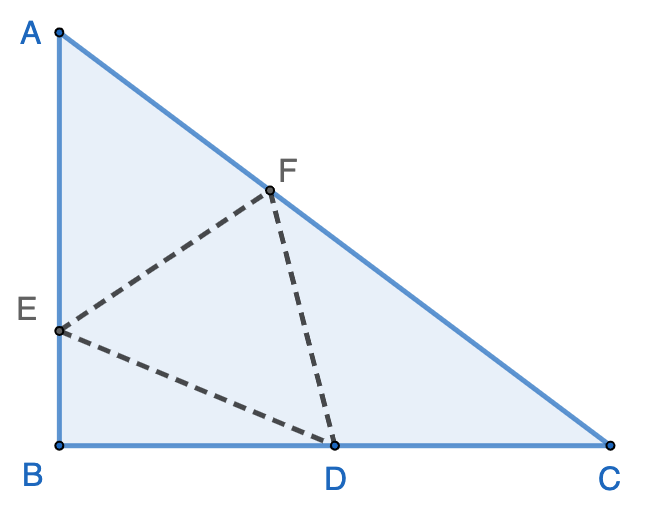
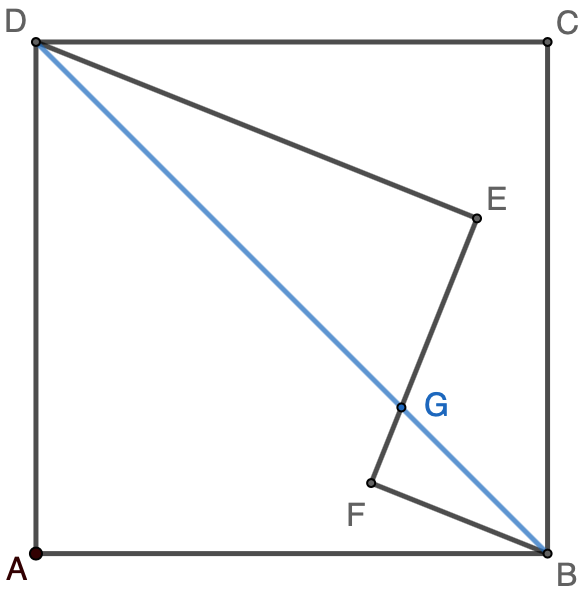Solution 1: Draw line $DB$, intersecting $EF$ at $G$. We have $\triangle{DEG}\sim\triangle{BFG}$.

$\therefore \dfrac{FG}{EG}=\dfrac{BF}{DE}=\dfrac{4}{10}$

$\because FG+EG=EF=6$

$\therefore FG=\dfrac{12}{7}$, and $EG=\dfrac{30}{7}$

$DG=\sqrt{DE^2+EG^2}=\sqrt{10^2+(\dfrac{30}{7})^2}=\dfrac{10}{7}\sqrt{58}$

$BG=\sqrt{BF^2+FG^2}=\sqrt{4^2+(\dfrac{12}{7})^2}=\dfrac{4}{7}\sqrt{58}$

$\therefore BD=DG+BG=\dfrac{10}{7}\sqrt{58}+\dfrac{4}{7}\sqrt{58}=2\sqrt{58}$

$\therefore$ Area of $ABCD=\dfrac{BD^2}{2}=\dfrac{(2\sqrt{58})^2}{2}=\boxed{116}$

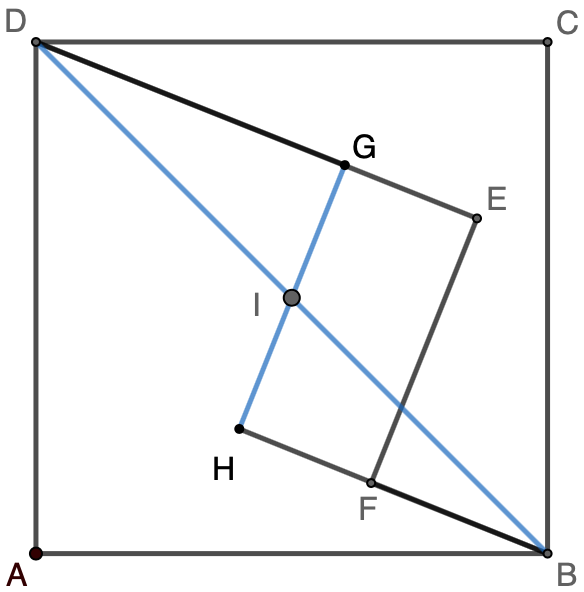Solution 2: Draw line $DB$. Point $G$ is on $DE$ so that $DG=6$. Extend $BF$ to $H$ so that $BH=6$. Draw line $GH$ intersecting $DB$ at $I$. We have $\triangle{DGI}\cong\triangle{BHI}$.

$\therefore GI=HI=\dfrac{1}{2}GH=\dfrac{1}{2}{EF}=3$

$\therefore DI^2=BI^2=DG^2+GI^2=6^2+3^2=58$

$\therefore$ Area of $ABCD=2\cdot DI^2=2\cdot 58=\boxed{116}$

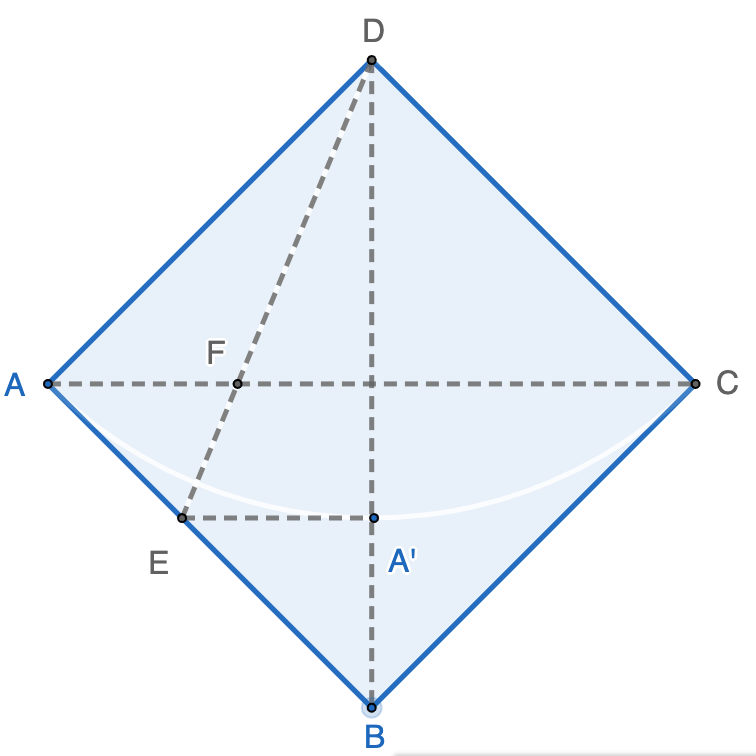
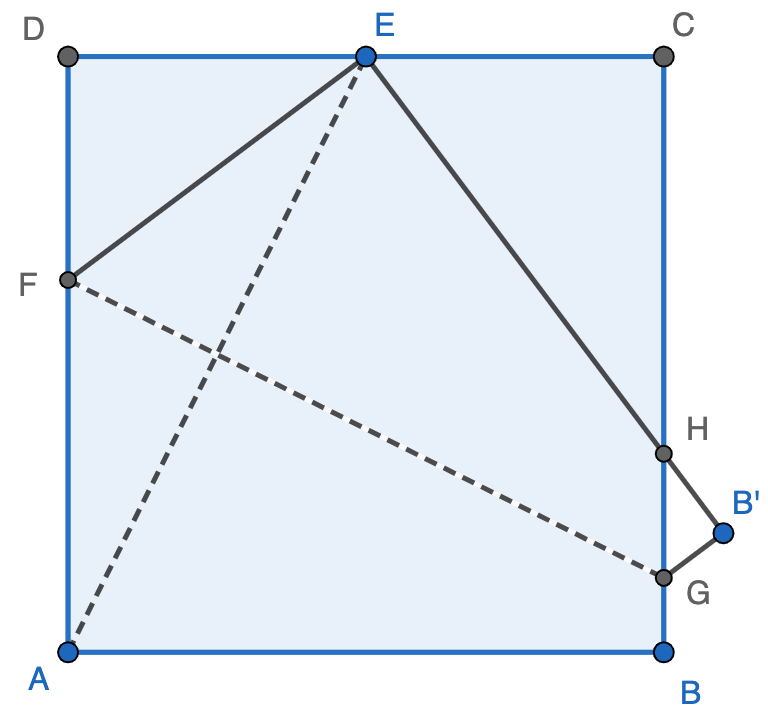
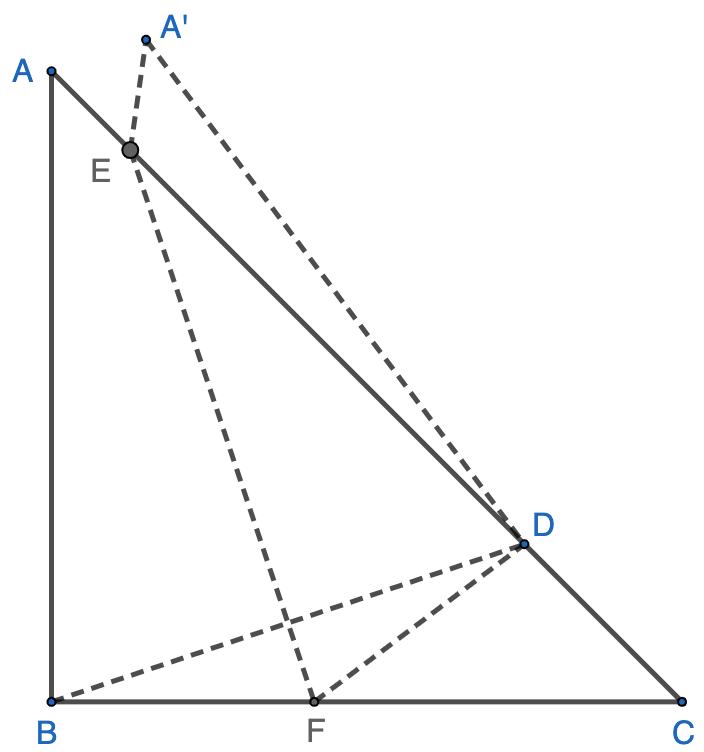
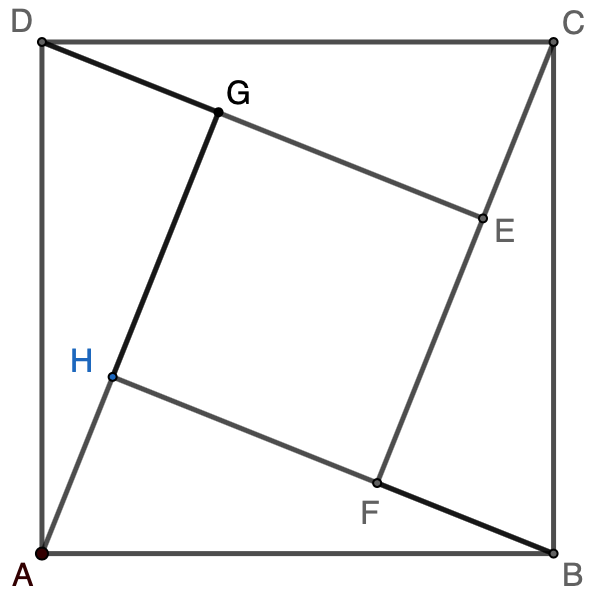Solution 3: Let point $G$ on $DE$ so that $GE=6$. Extend $BF$ to $H$ so that $FH=6$. Draw line $AH$ and $CE$.

$\therefore GE=EF=FH=GH=6$, and $EFGH$ is a square.

$\because B$, $F$, and $H$ are co-liner, $D$, $G,$ and $E$ are co-liner

$\therefore A$, $H$, and $G$ are co-linear, $C$, $E$, and $F$ are co-liner

$\therefore \triangle{ABH}\cong\triangle{BCF}\cong\triangle{CDE}\cong\triangle{DAG}$

$\therefore$ Area of $ABCD=EFHG+4\cdot\triangle{CDE}=EF^2+4\cdot\dfrac{DE\cdot CE}{2}=6^2+4\cdot\dfrac{4\cdot 10}{2}=\boxed{116}$

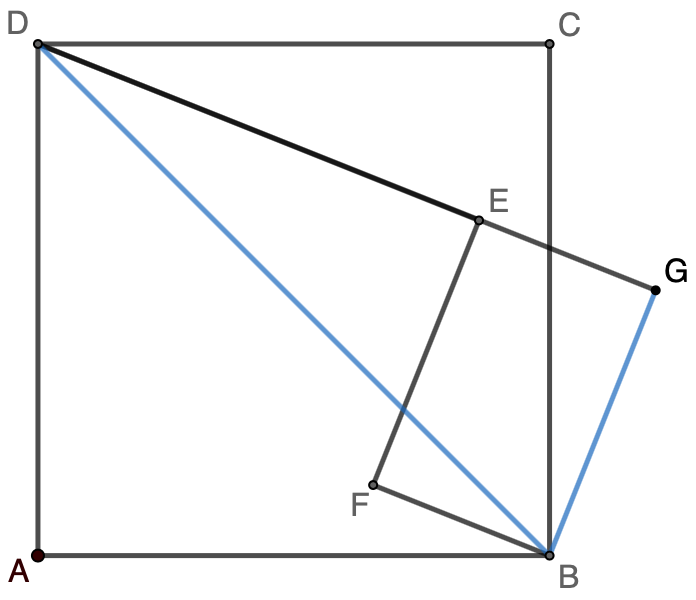Solution 4: Extend line $DE$ to $G$ so that $EG=4$. Draw line $BD$ and $BG$.

$\because EG=BF=4$ and $\angle{DEF}=\angle{BFE}=90^\circ$

$\therefore BGEF$ is a rectangle

$\therefore \triangle{BDG}$ is a right triangle

$\therefore BD^2=BG^2+DG^2=EF^2+(DE+EG)^2=6^2+(10+4)^2=232$

$\therefore$ Area of $ABCD=\dfrac{1}{2}\cdot BD^2=\dfrac{1}{2}\cdot 232=\boxed{116}$

Generalization: Point $E$ and $F$ are inside square $ABCD$, with $DE=a$, $EF=b$, $BF=c$, and $\angle{DEF}=\angle{BFE}=90^\circ$, then the area of the square $ABCD$ is $$ABCD=\boxed{\dfrac{(a+c)^2+b^2}{2}}$$

Extra: Andrew started at the entry point $D$, which is one corner of a square shaped maze $ABCD$, with the exit point $B$ directly across the diagonal of the square. The following is his track record:

He entered the maze at point $D$ and walked $20$ feet first along the path.
He changed his direction $90^\circ$ clock-wise and walked another $20$ feet.
He changed his direction $90^\circ$ counter-clock-wise and walked another $20$ feet
He repeated step 2 and step 3 two more times.
He repeated step 3 once again, then step 2 twice.
He changed his direction $90^\circ$ counter-clock-wise and walked $40$ feet to reach the exit point $B$.

Based on the above track record, calculate the area of the maze. Click here for the solution.

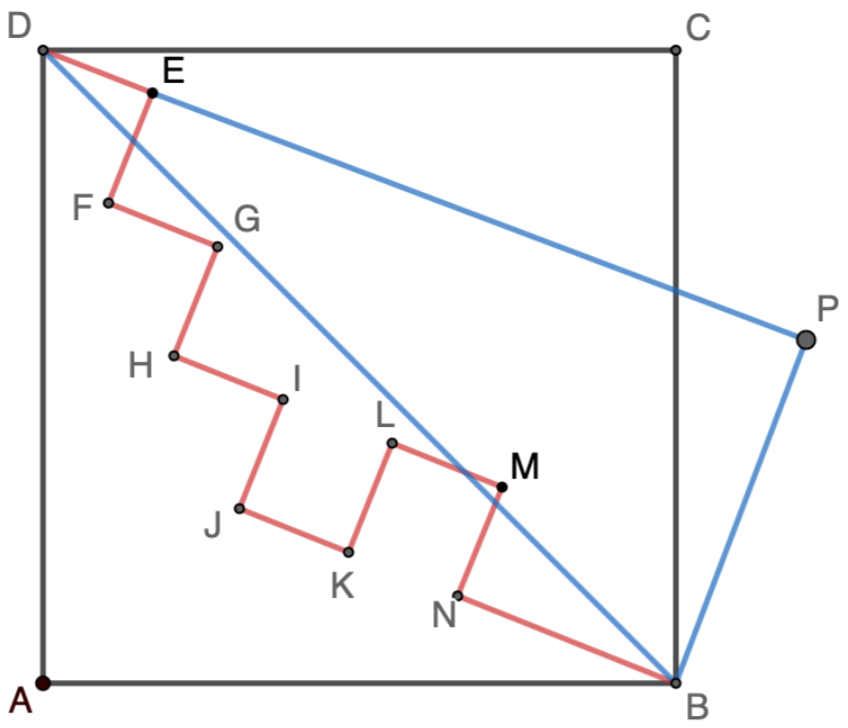Solution: Based on the track record, the net distance Andrew walked parallel to the initial path direction $DE$ is $140$ feet, and the net distance perpendicular to the initial path direction $DE$ is $60$ feet, as shown the diagram in the right. The length of the diagonal $BD$ of the square $ABCD$ is:

$BD=\sqrt{PD^2+PB^2}=\sqrt{140^2+60^2}=20\sqrt{58}$

Therefore, the area of $ABCD$ is:

$ABCD=\dfrac{BD^2}{2}=\dfrac{(20\sqrt{58})^2}{2}=\boxed{11600}$

Posted in Geometry, MATHCOUNTS | Comments Off

Sum and Product of All Factors

Posted on December 18, 2020 by kevin

For a nature number $$n=p_{1}^{q_{1}}\times p_{2}^{q_{2}}\times \cdots \times p_{m}^{q_{m}}$$ where $p_{i} (1 \le i \le m) $ are unique prime numbers.

The total number of positive factors of $n$ is $$f=(q_{1}+1)\times(q_{2}+1)\times\cdots\times(q_{m}+1)$$ The sum of all positive factors of $n$ is $$\sum_{d|n}d=\dfrac{p_{1}^{q_1 +1}-1}{ p_1 -1}\times \dfrac{p_{2}^{q_{2}+1}-1}{ p_{2}-1}\times \cdots \times\dfrac{p_{m}^{q_{m}+1}-1}{p_{m} -1}$$ The product of all positive factors of $n$ is $$\prod_{d|n}d=n^{\frac{f}{2}}$$ i.e. the $\dfrac{f}{2}th$ power of $n$, where $f$ is the total number of positive factors of $n$.

Question 1: A number is perfect if the sum of all positive factors is twice of the number. What is the sum of the first $4$ perfect numbers found by Euclid?

Question 2: A natural number is multiplicative perfect if the square of the number is the product of all positive factors. What is the sum of the $3$ smallest multiplicative perfect numbers greater than $1$?

Question 3: The sum of all positive factors of a natural number is 403. What is this number?

Question 4: What is the largest natural number less than $1000$ such that the product of all positive factors is the number raised to the $12$th power?

Posted in Algebra, Combinatorics | Comments Off

Cheat Sheet for Distributing $k$ Balls into $n$ Boxes

Posted on November 19, 2020 by kevin

Distribution of		Restriction
$k\text{ Balls}$	$n\text{ Boxes}$	None	$\le 1$	$\ge 1$	$=1$
$distinct$	$distinct$	$$n^k$$	$$(n)_k$$	$$n!S(k,n)$$	$$n!\text{ or }0$$
$identical$	$distinct$	$${n+k-1}\choose k$$	$$n\choose k$$	$${k-1}\choose{n-1}$$	$$1\text{ or }0$$
$distinct$	$identical$	$$\sum_{i=1}^{n}S(k,i)$$	$$1\text{ or }0$$	$$S(k,n)$$	$$1\text{ or }0$$
$identical$	$identical$	$$\sum_{i=1}^{n}P(k,i)$$	$$1\text{ or }0$$	$$P(k,n)$$	$$1\text{ or }0$$

$(n)_k=n(n-1)(n-2)…(n-k+1)=k!{n\choose k}$

$S(k, n)$ is a Stirling number of the second kind:

$$S(k,n)=\dfrac{1}{n!}\sum_{i=0}^{n}(-1)^{i}{{n}\choose{i}}(n-i)^k$$

$P(k, n)$ is the number of partitions of $k$ into $n$ parts

Posted in Combinatorics | Comments Off

Geometry Fold Problems

Posted on October 16, 2020 by kevin

A unit equilateral $\triangle{ABC}$ is folded over line $DE$, forming a quadrilateral $BCDE$, with $A$ touching $BC$ at $A’$, and $\triangle{BA’E}$ is a right triangle. The area of $BCDE$ is __________. Answer: $\dfrac{17\sqrt{3}-27}{8}\approx 0.305608$

A quarter-circle $ABC$, with its center at $A$ and its radius as $1$, is folded over $BD$, with its center touching the arc $BC$ at $A’$. The area of the resulting figure is __________. Answer: $\dfrac{3\pi-2\sqrt{3}}{12}\approx 0.49672$

Two opposite vertices $A$ and $C$ of a unit square $ABCD$ are folded toward the diagonal $BD$, forming a kite-shaped area $BEDF$. The area of the kite is __________.

Point $A$ of a unit square $ABCD$ is folded toward the diagonal $BD$ at point $A’$. Then, point $D$ is folded over $AC$, touching point $B$, resulting in a quadrilateral $BCFE$. The area of $BCFE$ is __________.

Point $A$ is the center of a quarter circle $ABC$ with radius as $1$. Point $D$ is the midpoint of $AB$. Point $C$ is folded over $EF$, touching point $D$, The length of $EF$ is __________. Answer: $\dfrac{2\sqrt{71}-3}{40}\sqrt{5} \approx 0.774367$

Point $A$ of unit square $ABCD$ is folded over $FG$, touching point $E$, which is the midpoint of $CD$. The length of $FG$ is __________. Answer: $\dfrac{\sqrt{5}}{2}$

A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $1$. The circle is folded over chord $BC$ and intersecting the diameter at $O$. The area bounded by $\overparen{AC}$, $AB$ and $BC$ is __________. Answer: $\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{4}$

A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $5$. The circle is folded over chord $BD$ and intersecting the diameter at $C$, and $\dfrac{AC}{BC}=\dfrac{1}{2}$. The length of $BD$ is __________ (PUMaC 2010).

A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $2$. The circle is folded over chord $CD$, tangent with the $AB$ at $E$, with $\dfrac{BE}{AE}=\dfrac{1}{3}$. The length of $CD$ is __________.

$\triangle{ABC}$ is a right triangle with $AB=BC=12$, and $\angle{ABC}=90^\circ$. $D$ is the midpoint of $BC$. Point $A$ is folded over $EF$ to touch point $D$. The length of $EF$ is __________.

$\triangle{ABC}$ is a right triangle with $AB=3$, $BC=4$, and $\angle{ABC}=90^\circ$. $D$ is the midpoint of $BC$. Point $A$ is folded over $EF$ to touch point $D$. The length of $EF$ in the simplest form is $\dfrac{a}{b}\sqrt{c}$, where $a$, $b$, and $c$ are integers. The value of $a+b+c$ is __________.

$\triangle{ABC}$ is a right triangle with $AB=BC=8$, and $\angle{ABC}=90^\circ$. $D$ is a point on $AC$ so that $\dfrac{CD}{AC}=\dfrac{1}{3}$. Point $B$ is folded over $EF$ to touch point $D$, resulting a concave polygon $A’EFCD$. The length of $EF$ is __________.

A pentagon was folded from a square of paper, as shown in the figure. At first the edges $BC$ and $DC$ were folded to the diagonal $AC$, so that the corners $B$ and $D$ lie on the diagonal and then the resulting shape was folded so that the vertex $C$ coincided with the vertex A. The value of the angle indicated by the question mark is __________.

A paper strip is folded three times as shown. If $\alpha=70^\circ$, then $\beta=$ __________ .

In a unit equalaterial $\triangle{ABC}$, point $A$ is folded to the point $D$ on $BC$ as shown, resulting in the crease $EF$ with $E$ on $AB$ and $F$ on $AC$. If $FD\perp BC$:

The value of $\angle{AED}$ is __________.
The length of $CD$ is __________.
The ratio of the areas of $\triangle{AEF}$ and $\triangle{ABC}$ is __________.

Posted in Geometry | Comments Off

MBMT 2020 – Problem 44

Posted on June 18, 2020 by kevin

Let $a_n=\sum_{d|n}\dfrac{1}{2^{d+\frac{n}{d}}}$. In other words, $a_n$ is the sum of $\dfrac{1}{2^{d+\frac{n}{d}}}$ over all divisers $d$ of $n$. Find $$\dfrac{\sum_{k=1}^{\infty}ka_k}{\sum_{k=1}^{\infty}a_k}=\dfrac{a_1+2a_2+3a_3+…}{a_1+a_2+a_3+…}$$

Click here for the solution.

Posted in Algebra | Comments Off

MATHCOUNTS Exercise – 22

Sum and Product of All Factors

Cheat Sheet for Distributing $k$ Balls into $n$ Boxes

Geometry Fold Problems

MBMT 2020 – Problem 44

Archives

Meta

Categories