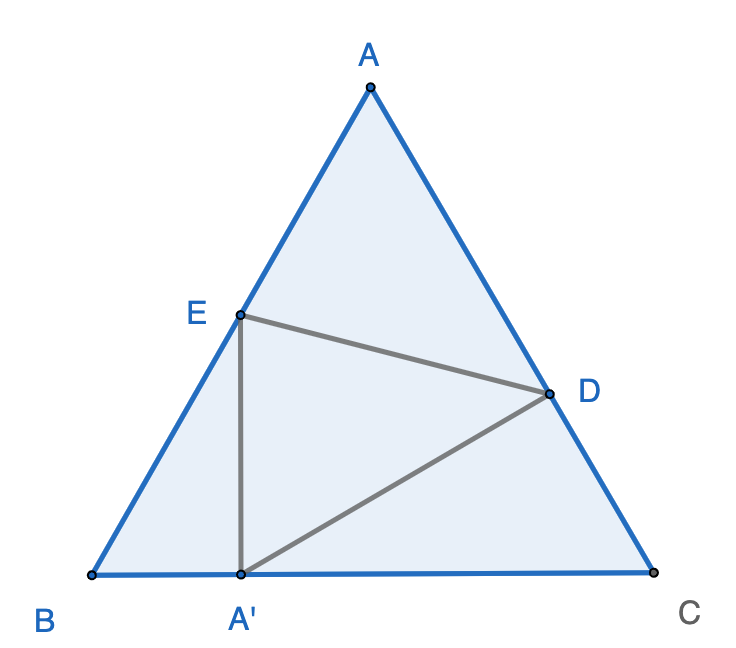
A unit equilateral $\triangle{ABC}$ is folded over line $DE$, forming a quadrilateral $BCDE$, with $A$ touching $BC$ at $A’$, and $\triangle{BA’E}$ is a right triangle. The area of $BCDE$ is __________. Answer: $\dfrac{17\sqrt{3}-27}{8}\approx 0.305608$
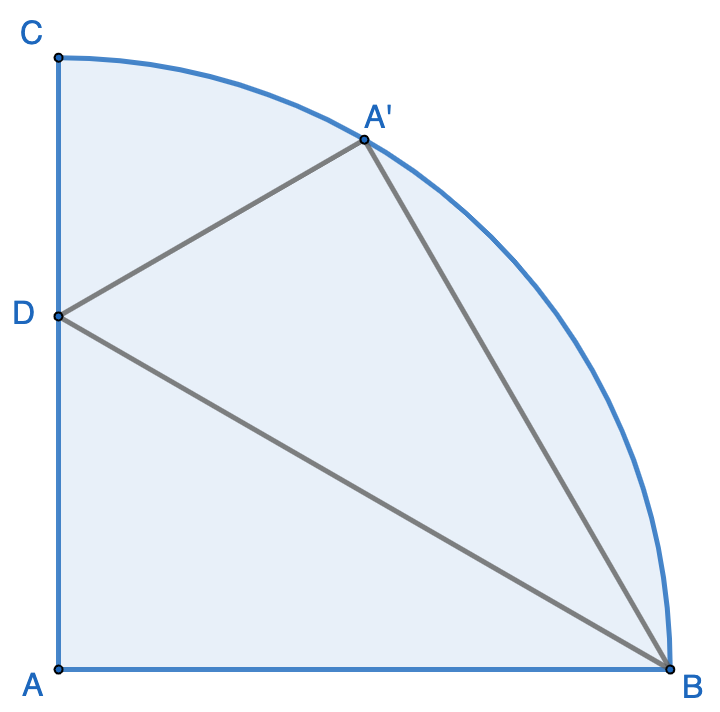
A quarter-circle $ABC$, with its center at $A$ and its radius as $1$, is folded over $BD$, with its center touching the arc $BC$ at $A’$. The area of the resulting figure is __________. Answer: $\dfrac{3\pi-2\sqrt{3}}{12}\approx 0.49672$
Two opposite vertices $A$ and $C$ of a unit square $ABCD$ are folded toward the diagonal $BD$, forming a kite-shaped area $BEDF$. The area of the kite is __________.
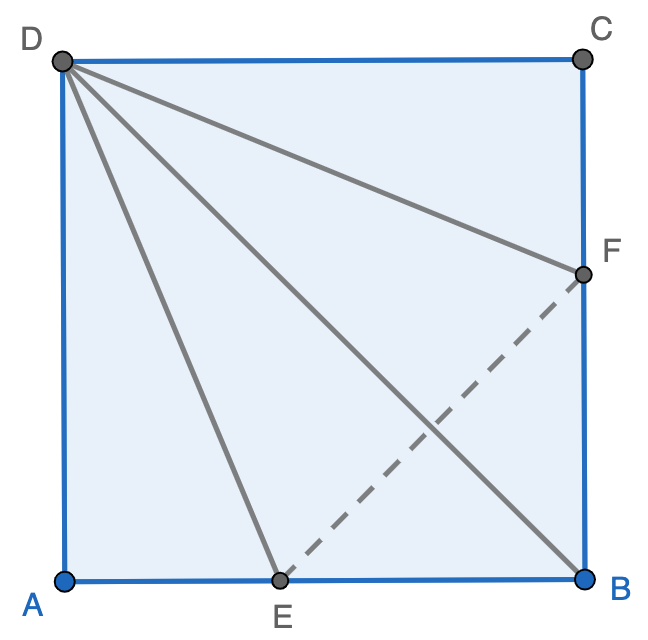
Point $A$ of a unit square $ABCD$ is folded toward the diagonal $BD$ at point $A’$. Then, point $D$ is folded over $AC$, touching point $B$, resulting in a quadrilateral $BCFE$. The area of $BCFE$ is __________.
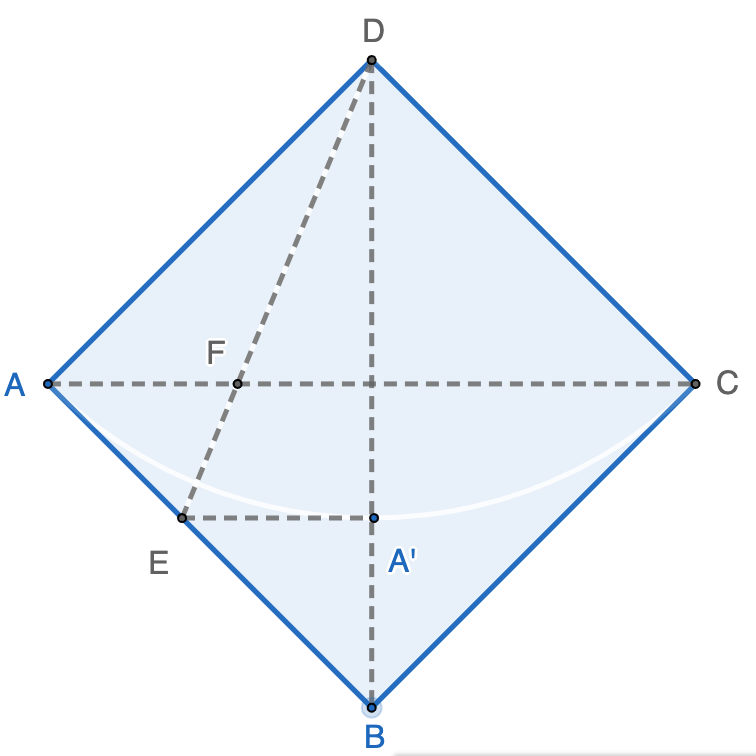
Point $A$ is the center of a quarter circle $ABC$ with radius as $1$. Point $D$ is the midpoint of $AB$. Point $C$ is folded over $EF$, touching point $D$, The length of $EF$ is __________. Answer: $\dfrac{2\sqrt{71}-3}{40}\sqrt{5} \approx 0.774367$
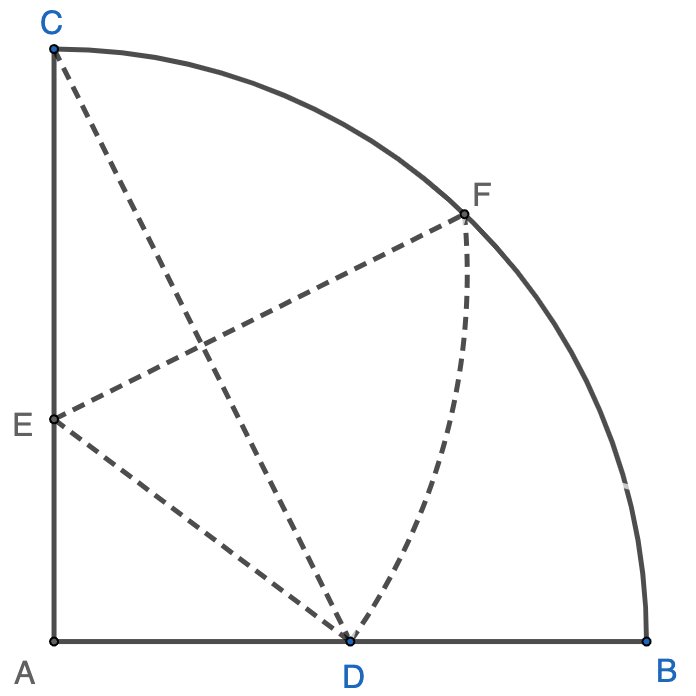
Point $A$ of unit square $ABCD$ is folded over $FG$, touching point $E$, which is the midpoint of $CD$. The length of $FG$ is __________. Answer: $\dfrac{\sqrt{5}}{2}$
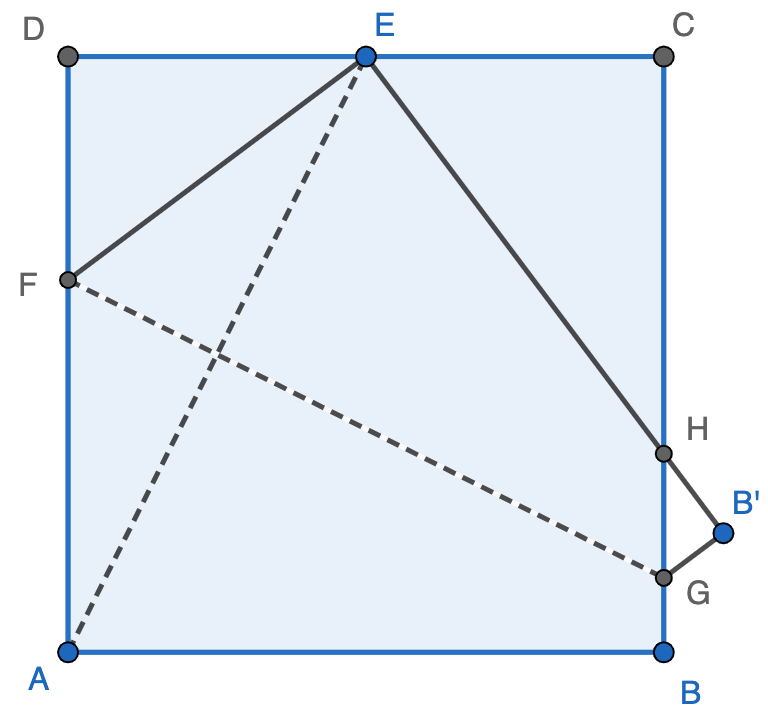
A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $1$. The circle is folded over chord $BC$ and intersecting the diameter at $O$. The area bounded by $\overparen{AC}$, $AB$ and $BC$ is __________. Answer: $\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{4}$
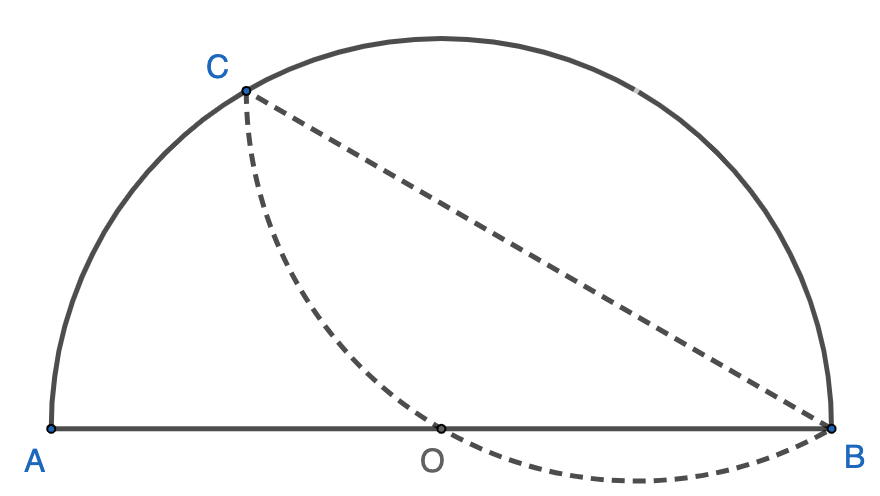
A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $5$. The circle is folded over chord $BD$ and intersecting the diameter at $C$, and $\dfrac{AC}{BC}=\dfrac{1}{2}$. The length of $BD$ is __________ (PUMaC 2010).
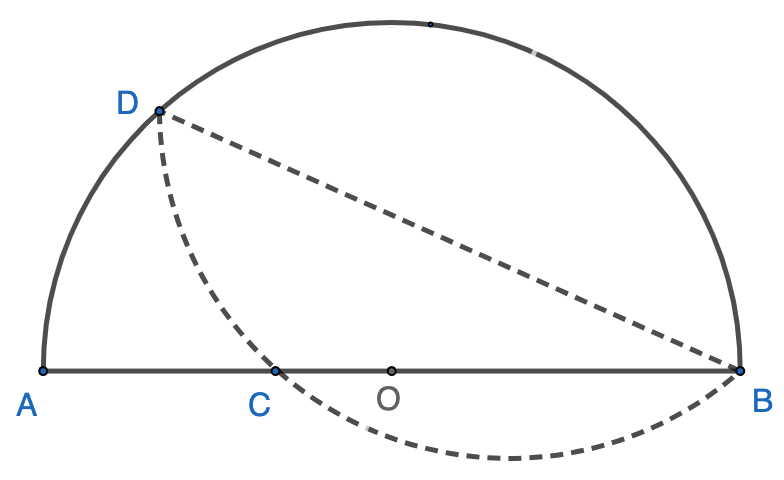
A semi-circle with $AB$ as its diameter, point $O$ as its center, and its radius as $2$. The circle is folded over chord $CD$, tangent with the $AB$ at $E$, with $\dfrac{BE}{AE}=\dfrac{1}{3}$. The length of $CD$ is __________.
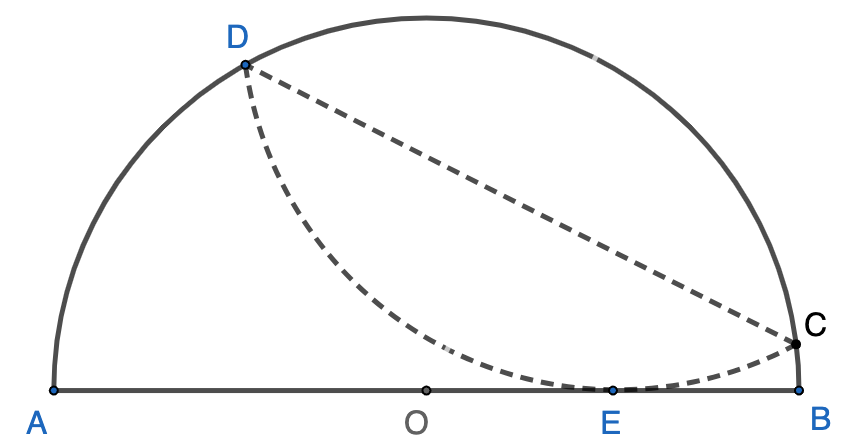
$\triangle{ABC}$ is a right triangle with $AB=BC=12$, and $\angle{ABC}=90^\circ$. $D$ is the midpoint of $BC$. Point $A$ is folded over $EF$ to touch point $D$. The length of $EF$ is __________.
$\triangle{ABC}$ is a right triangle with $AB=3$, $BC=4$, and $\angle{ABC}=90^\circ$. $D$ is the midpoint of $BC$. Point $A$ is folded over $EF$ to touch point $D$. The length of $EF$ in the simplest form is $\dfrac{a}{b}\sqrt{c}$, where $a$, $b$, and $c$ are integers. The value of $a+b+c$ is __________.
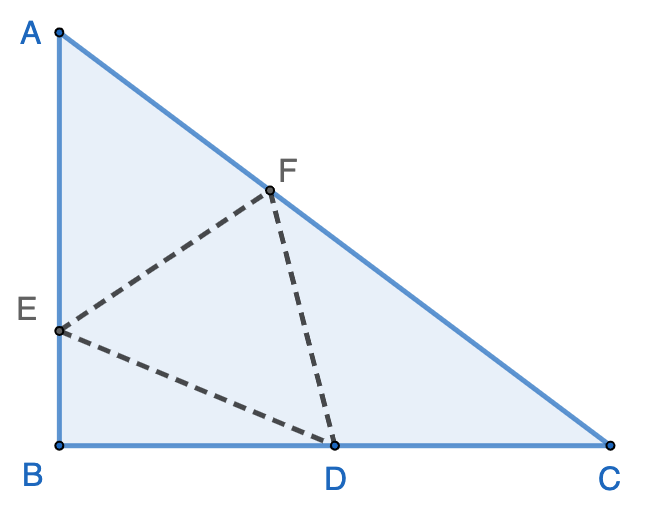
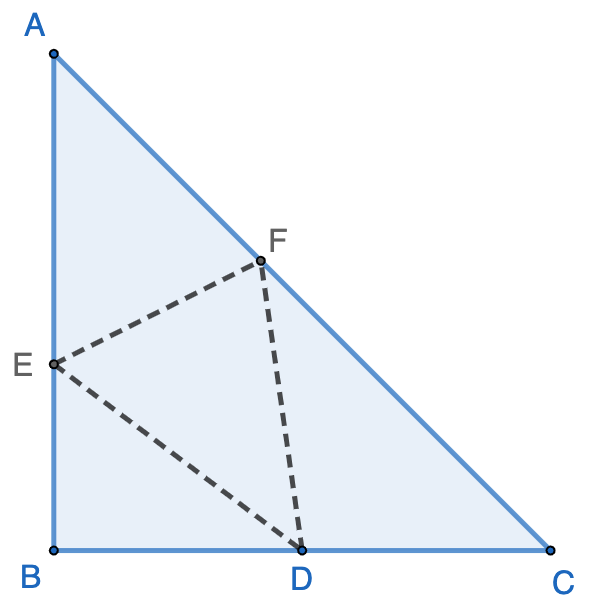
$\triangle{ABC}$ is a right triangle with $AB=BC=8$, and $\angle{ABC}=90^\circ$. $D$ is a point on $AC$ so that $\dfrac{CD}{AC}=\dfrac{1}{3}$. Point $B$ is folded over $EF$ to touch point $D$, resulting a concave polygon $A’EFCD$. The length of $EF$ is __________.
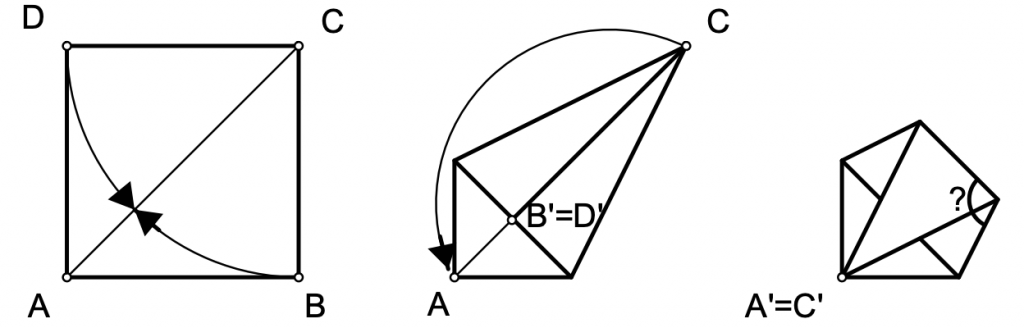
A pentagon was folded from a square of paper, as shown in the figure. At first the edges $BC$ and $DC$ were folded to the diagonal $AC$, so that the corners $B$ and $D$ lie on the diagonal and then the resulting shape was folded so that the vertex $C$ coincided with the vertex A. The value of the angle indicated by the question mark is __________.
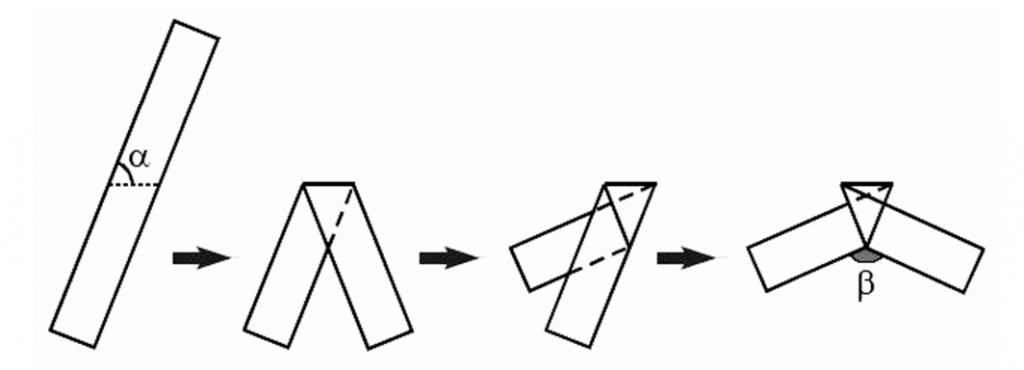
A paper strip is folded three times as shown. If $\alpha=70^\circ$, then $\beta=$ __________ .
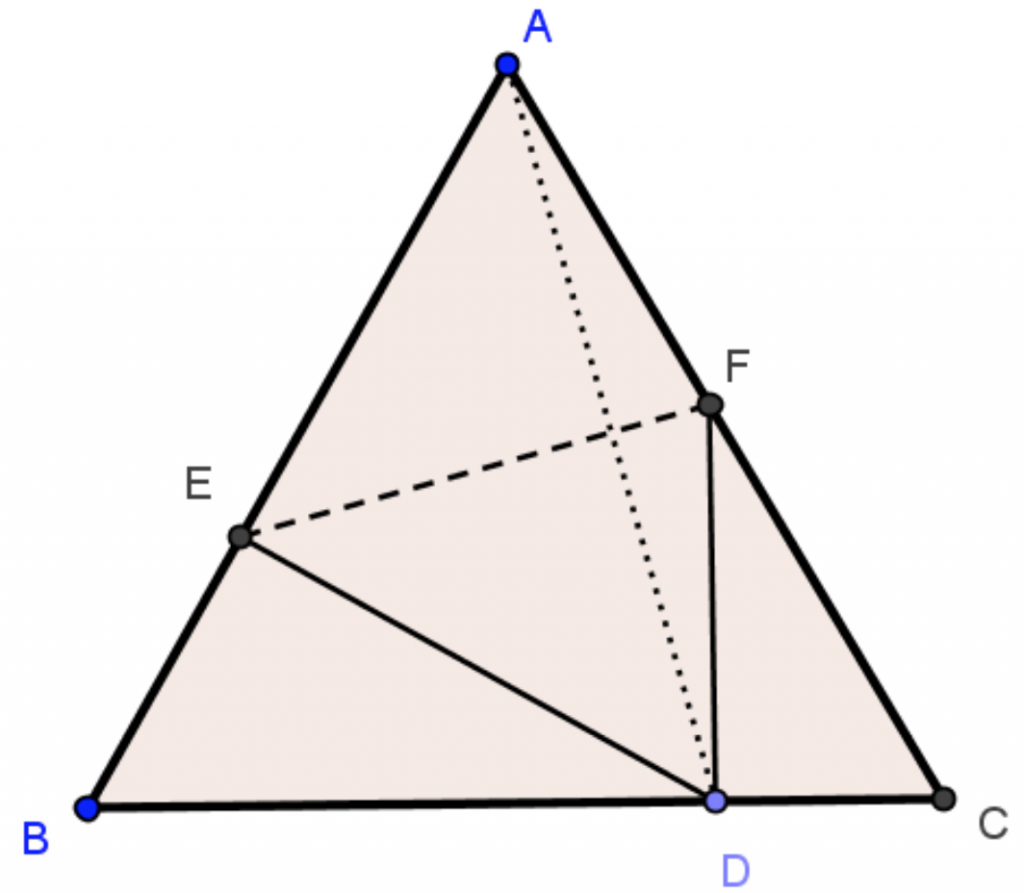
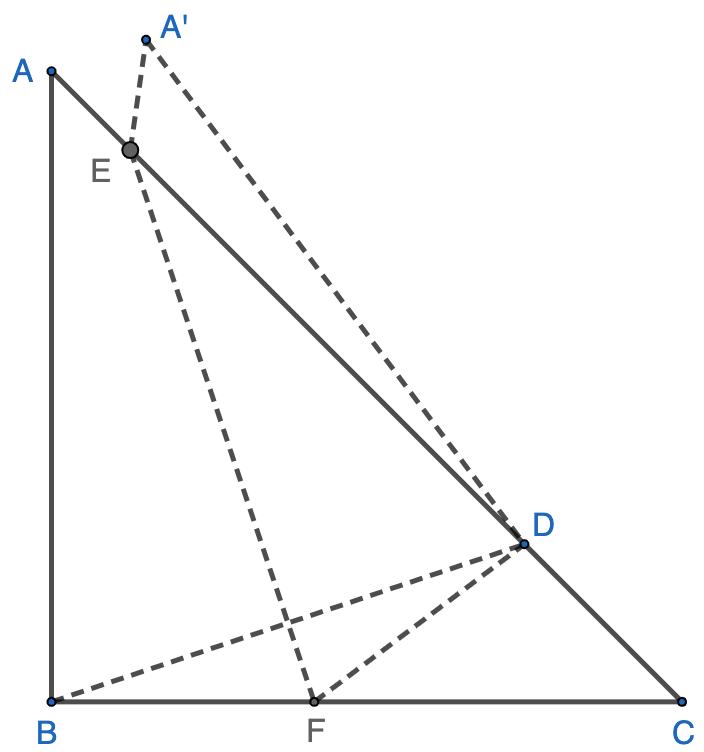
In a unit equalaterial $\triangle{ABC}$, point $A$ is folded to the point $D$ on $BC$ as shown, resulting in the crease $EF$ with $E$ on $AB$ and $F$ on $AC$. If $FD\perp BC$:
- The value of $\angle{AED}$ is __________.
- The length of $CD$ is __________.
- The ratio of the areas of $\triangle{AEF}$ and $\triangle{ABC}$ is __________.