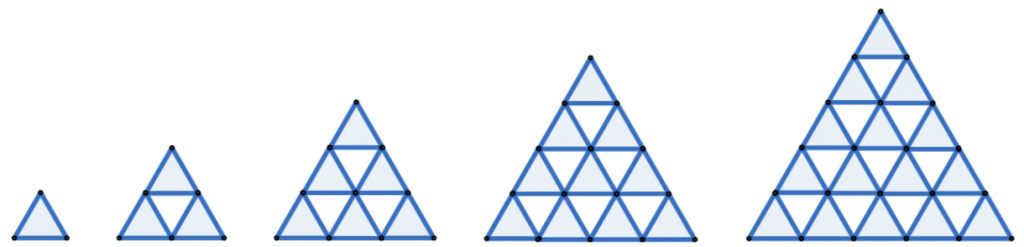
Given that the value of $$\sum_{k=1}^{2021}\dfrac{1}{1^2+2^2+3^2+…+k^2} + \sum_{k=1}^{1010}\dfrac{6}{2k^2-k} + \sum_{k=1011}^{2021}\dfrac{24}{2k+1}$$ can be expressed as $\dfrac{n}{m}$, where $m$ and $n$ are relatively prime positive integers, find $m+n$.
Click here for the solution.-
Archives
- October 2025
- September 2025
- August 2025
- July 2025
- June 2025
- May 2025
- April 2025
- March 2025
- February 2025
- January 2025
- December 2024
- November 2024
- October 2024
- September 2024
- August 2024
- July 2024
- June 2024
- May 2024
- April 2024
- March 2024
- February 2024
- January 2024
- November 2023
- October 2023
- September 2023
- August 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- May 2021
- April 2021
- March 2021
- January 2021
- December 2020
- November 2020
- October 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
-
Meta