$\triangle{ABC}$ has a right angle at $B$, $AB = 12$, and $BC = 16$. Let $M$ be the midpoint of $AC$. Let $ω_1$ be the incircle of $\triangle{ABM}$ and $ω_2$ be the incircle of $\triangle{BCM}$. The line externally tangent to $ω_1$ and $ω_2$ that is not $AC$ intersects $AB$ and $BC$ at $X$ and $Y$, respectively. If the area of $\triangle{BXY}$ can be expressed as $\dfrac{m}{n}$, compute $m+n$.
Solution: Draw various line segments as the following, with various $3-4-5$ right triangles.
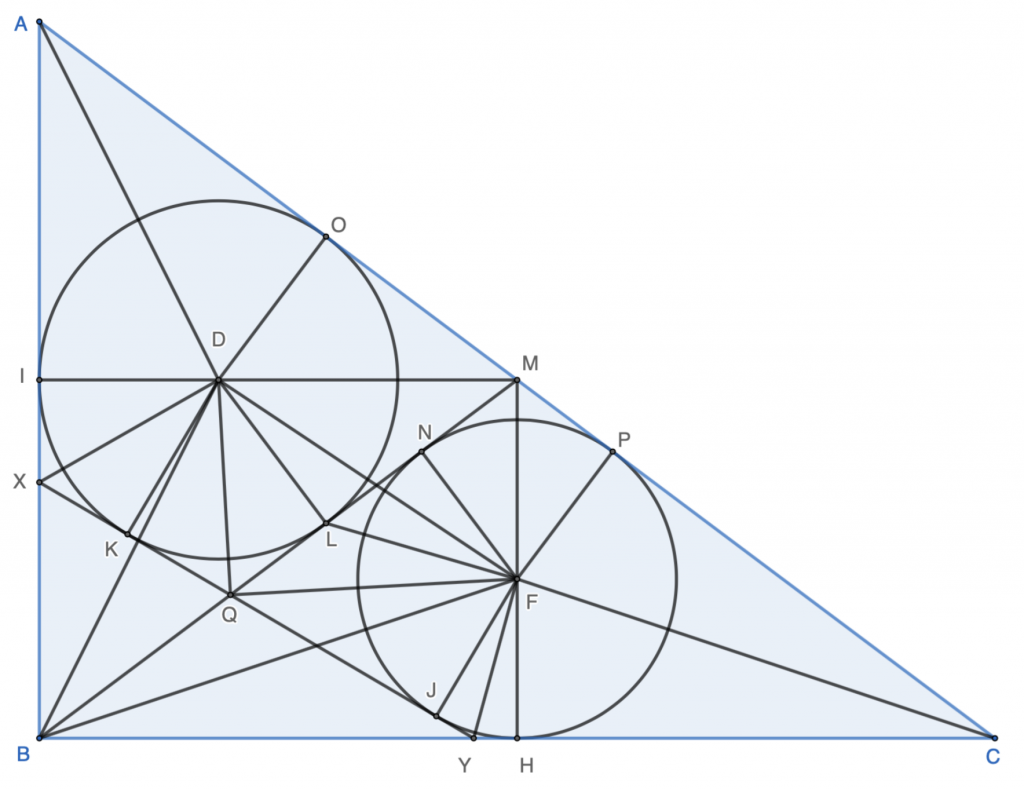
Let the radius of $ω_1$ as $r_1$, and we have $$r_1=\dfrac{Area\ of\ \triangle{ABM}}{\dfrac{AB+BM+MA}{2}}=\dfrac{Area\ of\ \triangle{ABC}}{AB+BM+MA}=\dfrac{\dfrac{1}{2}\cdot 12\cdot 16}{12+10+10}=3$$ Similarly, we have the radius of $ω_2$ as $r_2=\dfrac{8}{3}$.
$$\because OP=MO+MP=ML+MN=MN+LN+MN=2MN+LN$$ $$JK=QK+QJ=QL+QN=QL+QL+LN=2QL+LN$$ $$OP=JK$$
$$\therefore 2MN+LN=2QL+LN, QL=MN$$
$$\because MN=MP=MC-CP=MC-CH=\dfrac{1}{2}AC-\dfrac{1}{2}BC=2$$ $$\therefore KQ=LQ=2, LN=ML-LN=\dfrac{ML}{DL}\cdot DL-2=\dfrac{4}{3}\cdot 3-2=2$$
Method 1 – Using Trigonometry: $$\tan{\angle{KDL}}=\tan{(2\angle{KDQ})}=\dfrac{2\tan{\angle{KDQ}}}{1-\tan^2{\angle{KDQ}}}=\dfrac{2\cdot\dfrac{2}{3}}{1-(\dfrac{2}{3})^2}=\dfrac{12}{5}$$
$$\tan{\angle{IDK}}=\tan{(180^\circ-\angle{KDM})}=-\tan{\angle{KDM}} =-\tan{(\angle{KDL}+\angle{LDM})}$$
$$=-\dfrac{\tan{\angle{KDL}}+\tan{\angle{LDM}}}{1-\tan\angle{KDL}\cdot\tan\angle{LDM}}=-\dfrac{\dfrac{12}{5}+\dfrac{4}{3}}{1-\dfrac{12}{5}\cdot\dfrac{4}{3}}=\dfrac{56}{33}$$
$$\sin{\angle{IDK}}=\dfrac{56}{\sqrt{56^2+33^2}}=\dfrac{56}{65}, \cos{\angle{IDK}}=\dfrac{33}{\sqrt{56^2+33^2}}=\dfrac{33}{65}$$
$$\tan{\angle{IDX}}=\tan{\dfrac{\angle{IDK}}{2}}=\dfrac{\sin{\angle{IDK}}}{1+\cos{\angle{IDK}}}=\dfrac{\dfrac{56}{65}}{1+\dfrac{33}{65}}=\dfrac{4}{7}$$
$$BX=BI-IX=\dfrac{1}{2}\cdot AB-ID\cdot\tan{\angle{IDX}}=6-3\cdot\dfrac{4}{7}=\dfrac{30}{7} \tag{1}$$
$$\because \angle{IDK}+\angle{KDF}+\angle{FDM}=180^\circ\ , \angle{HFJ}+\angle{JFD}+\angle{DFM}=180^\circ$$
$$\therefore (\angle{IDK}+\angle{KDF}+\angle{FDM})+(\angle{HFJ}+\angle{JFD}+\angle{DFM})=360^\circ$$
$$\therefore (\angle{IDK}+\angle{HFJ})+(\angle{KDF}+\angle{JFD})+(\angle{FDM}+\angle{DFM})=360^\circ$$
$$\because \angle{KDF}+\angle{JFD}=360^\circ-(\angle{DKJ}+\angle{FJK})=360^\circ-(90^\circ+90^\circ)=180^\circ, \angle{FDM}+\angle{DFM}=90^\circ$$
$$\therefore \angle{IDK}+\angle{HFJ}=90^\circ$$
$$\therefore \angle{IDX}+\angle{HFY}=45^\circ$$
$$\therefore \tan{\angle{HFY}}=\tan(45^\circ-\angle{IDX})=\dfrac{\tan{45^\circ}-\tan{\angle{IDX}}}{1+\tan{45^\circ}\cdot\tan{\angle{IDX}}}=\dfrac{1-\dfrac{4}{7}}{1+1\cdot \dfrac{4}{7}}=\dfrac{3}{11}$$
$$\therefore BY=BH-BY=\dfrac{1}{2}BC-FH\cdot\tan{\angle{HFY}}=8-\dfrac{8}{3}\cdot\dfrac{3}{11}=\dfrac{80}{11} \tag{2}$$
Based on $(1)$ and $(2)$, the area of $\triangle{BXY}$ is: $\dfrac{1}{2}\cdot BX\cdot BY=\dfrac{1}{2}\cdot\dfrac{30}{7}\cdot\dfrac{80}{11}=\dfrac{1200}{77}$.
Therefore, $m+n=1200+77=\boxed{1277}$.
Method 2 – Using Menelaus’s Theorem: Extend both tangent lines $AC$ and $XY$ so that they intersect at $Z$. Draw line $DZ$, and $D$, $F$ and $Z$ are co-line, as $D$ and $F$ are centers of circles $ω_1$ and $ω_2$, respectively, and $Z$ is the intersection point of two external tangent lines of both circles $ω_1$ and $ω_2$.
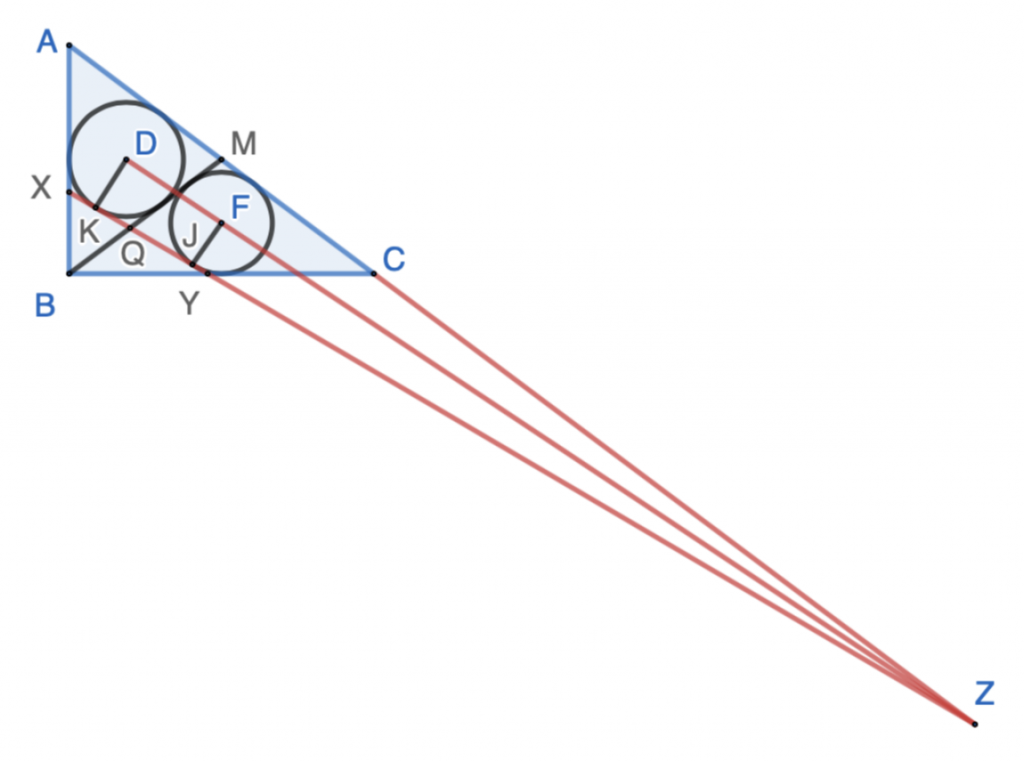
$$\because \angle{DKZ}=\angle{FJZ}=90^\circ, \triangle{DKZ}\sim \triangle{FJZ}$$
$$\therefore \dfrac{KZ}{JZ}=\dfrac{DK}{FJ}=\dfrac{r_1}{r_2}=\dfrac{3}{\dfrac{8}{3}}=\dfrac{9}{8}$$
$$\because KZ=KJ+JZ=KQ+QJ+YZ=KQ+QL+LN+JZ=2+2+2+JZ=JZ+6$$
$$\therefore \dfrac{JZ+6}{JZ}=\dfrac{9}{8}, JZ=48, KZ=OZ=JZ+6=54$$
$$\therefore MZ=OZ-OM=54-4=50, AZ=MZ+AM=50+10=60, CZ=MZ-MC=50-10=40$$
According to Menelaus’s Theorem, we have:
$$\dfrac{AZ}{MZ}\cdot\dfrac{MQ}{QM}\cdot\dfrac{BX}{XA}=1, \dfrac{MZ}{CZ}\cdot\dfrac{CY}{BY}\cdot\dfrac{BQ}{QM}=1$$
$$\therefore \dfrac{60}{50}\cdot\dfrac{6}{4}\cdot\dfrac{BX}{12-BX}=1, \dfrac{50}{40}\cdot\dfrac{16-BY}{BY}\cdot\dfrac{4}{6}=1$$
$$\therefore AX=\dfrac{30}{7}, BY=\dfrac{80}{11}$$
Therefore, the area of $\triangle{BXY}$ is: $\dfrac{1}{2}\cdot BX\cdot BY=\dfrac{1}{2}\cdot\dfrac{30}{7}\cdot\dfrac{80}{11}=\dfrac{1200}{77}$.
Therefore, $m+n=1200+77=\boxed{1277}$.
