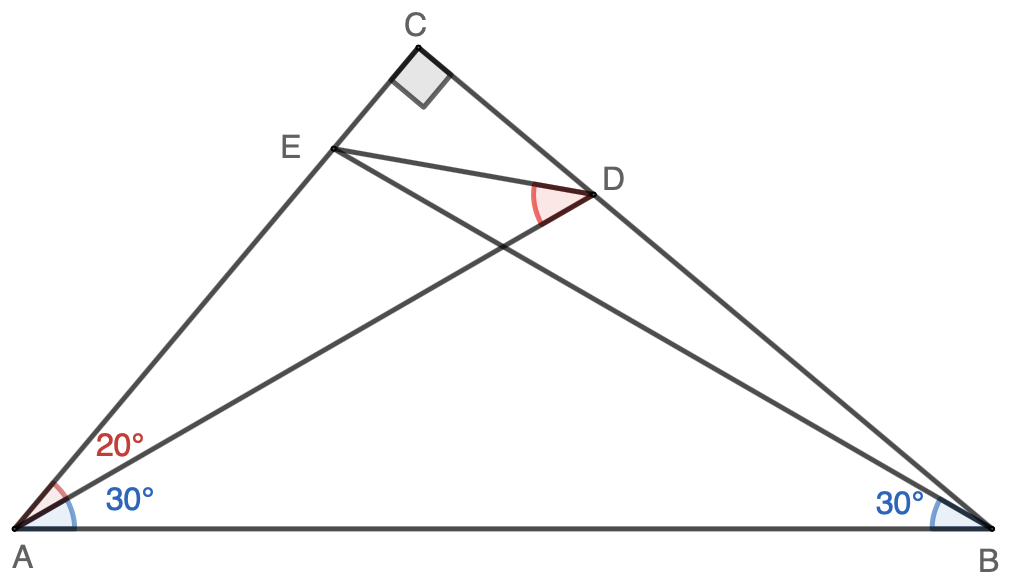
$\triangle{ABC}$ is a right triangle, with $\angle{ACB}=90^\circ$ and $\angle{BAC}=50^\circ$. Point $D$ and $E$ are on line $BC$ and $AC$ respectively, so that $\angle{BAD}=\angle{ABE}=30^\circ$. Connect $D$ and $E$, find the value of $\angle{ADE}$. Click here for the solution.
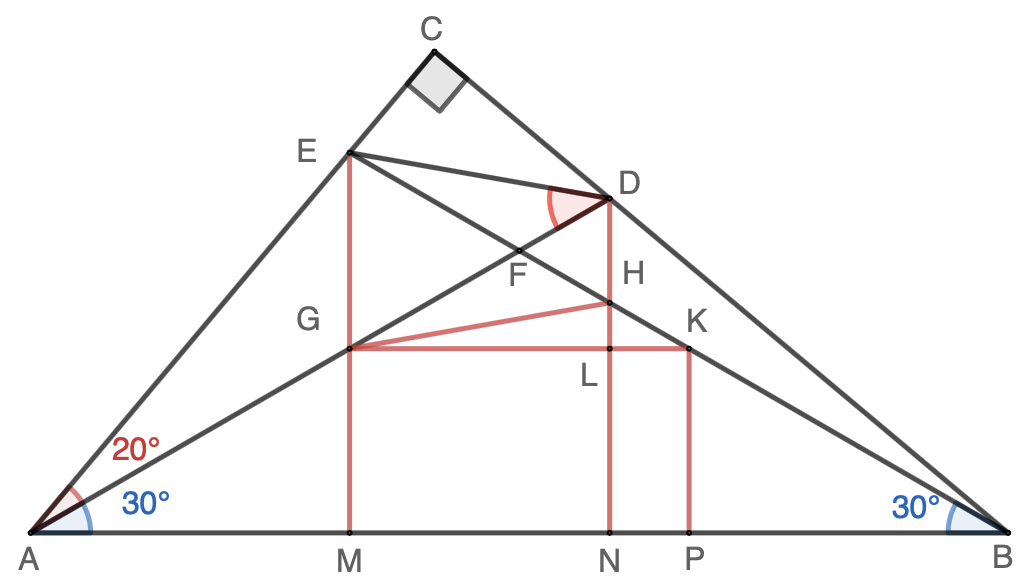
Solution: Let $AD$ and $BE$ intersect at point $F$. Let $M$ and $N$ on line $AB$ so that $EM\perp AB$, $DN\perp AB$. Let $EM$ intersect $AD$ at $G$, $DN$ interset $BE$ at $H$. Additionally, let $GK \parallel AB$ and intersect $DN$ at $H$, and $KP\perp AB$.
It is trivial to show that $\triangle{EFG}$ and $\triangle{DFH}$ are equilateral, $\triangle{DEF}$ and $\triangle{HGF}$ are congrunt. And $$\angle{ADE}=\angle{EHG}=\angle{HGK}+\angle{HKG}=\angle{HGL}+30^\circ \tag{1}$$ Additionally $$\tan{\angle{HGL}}=\dfrac{HL}{GL}=\dfrac{LK\cdot\tan{\angle{HKL}}}{MN}=\dfrac{NP\cdot\tan{30^\circ}}{MN}$$ $$=\dfrac{(NB-PB)\cdot\tan{30^\circ}}{MN}=\dfrac{NB-AM}{\sqrt{3}\cdot MN}\tag{2}$$
Furthermore $$AM+MN+NB=AB$$ $$EM=AM\cdot\tan{50^\circ}=(MN+NB)\cdot\tan{30^\circ}=\dfrac{MN+NB}{\sqrt{3}}$$ $$DN=NB\cdot\tan{40^\circ}=(AM+MN)\cdot\tan{30^\circ}=\dfrac{AM+MN}{\sqrt{3}}$$
Without loss of generality, let $AB=1$, and let $x=AM$, $y=MN$, and $z=NB$, we have $$x+y+z=1$$ $$x\cdot\tan{50^\circ}=\dfrac{y+z}{\sqrt{3}}$$ $$z\cdot\tan{40^\circ}=\dfrac{x+y}{\sqrt{3}}$$ Therefore $\dfrac{1}{x}=1+\sqrt{3}\cdot\tan{50^\circ}$ and $\dfrac{1}{z}=1+\sqrt{3}\cdot\tan{40^\circ}$
According to $(2)$, we have $$\tan{\angle{HGL}}=\dfrac{z-x}{\sqrt{3}\cdot y}=\dfrac{z-x}{\sqrt{3}\cdot(1-x-z)}=\dfrac{\dfrac{1}{x}-\dfrac{1}{z}}{\sqrt{3}\cdot(\dfrac{1}{x}\cdot\dfrac{1}{z}-\dfrac{1}{x}-\dfrac{1}{z})}$$ $$=\dfrac{(1+\sqrt{3}\cdot\tan{50^\circ})-(1+\sqrt{3}\cdot\tan{40^\circ})}{\sqrt{3}\cdot((1+\sqrt{3}\cdot\tan{50^\circ})\cdot(1+\sqrt{3}\cdot\tan{40^\circ})-(1+\sqrt{3}\cdot\tan{50^\circ})-(1+\sqrt{3}\cdot\tan{40^\circ}))}$$ $$=\dfrac{\tan{50^\circ}-\tan{40^\circ}}{3\cdot\tan{50^\circ}\cdot\tan{40^\circ}-1}=\dfrac{\tan{50^\circ}-\tan{40^\circ}}{2\cdot\tan{50^\circ}\cdot\tan{40^\circ}-1+\tan{50^\circ}\cdot\tan{40^\circ}}$$ $$=\dfrac{\tan{50^\circ}-\tan{40^\circ}}{1+\tan{50^\circ}\cdot\tan{40^\circ}}=\tan{(50^\circ-40^\circ)}=\tan{10^\circ}$$
Therefore, $\angle{HGL}=10^\circ$. Based on $(1)$, we have $\angle{ADE}=10^\circ+30^\circ=\boxed{40^\circ}$
