MathFun4Kids

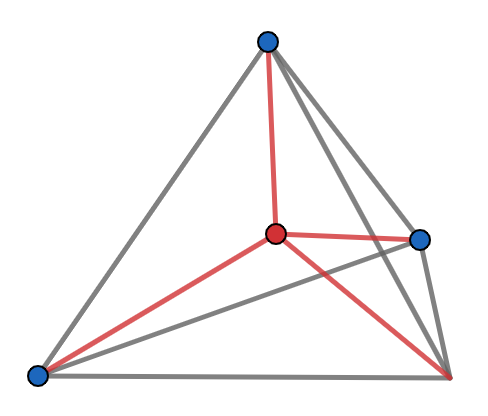
By adding one more quarter circle, we have the following figure. The question is: what is the area of the region bounded by arc $\stackrel \frown {AE}$, $\stackrel \frown {EF}$ and $\stackrel \frown {FA}$?

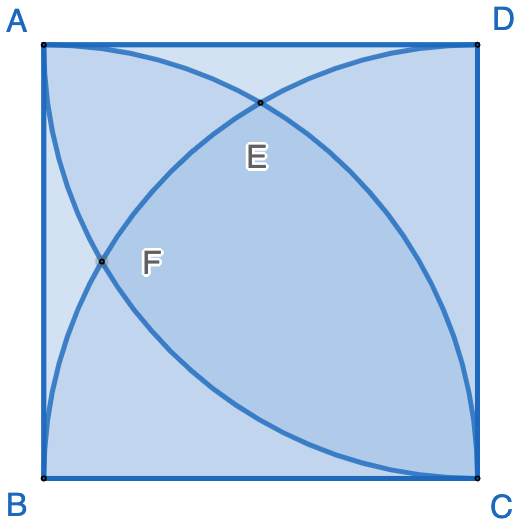
In fact, based on the calculations in the previous posts in this series, we have: $$ [AEF]=1−[BCD]−[ADE]−[ABF] $$ $$ =1-\dfrac{\pi}{4}-2\cdot(1-\dfrac{\sqrt{3}}{4}-\dfrac{\pi}{6})=\dfrac{\pi}{12}+\dfrac{\sqrt{3}}{2}-1 $$

If one more quarter circle is added, shown as the following figure, what is the area of the region in the middle bounded by arc $\stackrel \frown{EF}$, $\stackrel \frown{FG}$, $\stackrel \frown{GH}$, and $\stackrel \frown{HE}$?

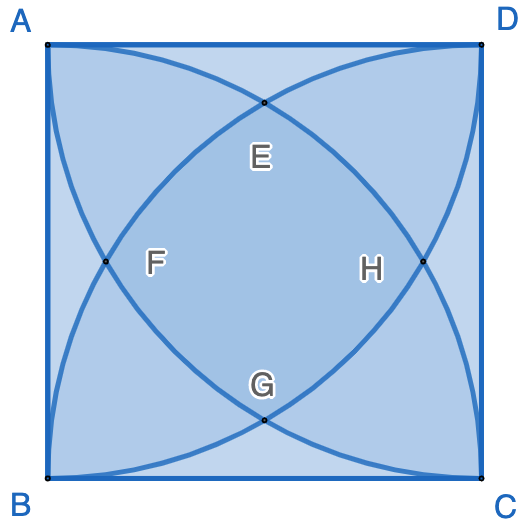
Again, based on the previous calculations, we have: $$[EFGH]=1-4\cdot([ADE] + [AEF]) $$ $$=1-4\cdot((1-\dfrac{\sqrt{3}}{4}-\dfrac{\pi}{6}) + (\dfrac{\pi}{12}+\dfrac{\sqrt{3}}{2}-1)) = 1-\sqrt{3}+\dfrac{\pi}{3} $$

Can you solve the problem without using the previous calculations? To be continued…

Continuing this topic, look at the following diagram, with two quarter circles in a unit square, the question is: what are the area of of each of the 4 regions inside the square?

To answer the question, we need to draw line $\overline{BE}$ and $\overline{CE}$, as shown in the following diagram:

Obviously, $\triangle{BCE}$ is an equalateral triangle, with its area as $\sqrt{3}{4}$. Additionally, the size of the fan-shaped area $[CBE]$ and $[BCE]$ is $\dfrac{\pi}{6}$. The area of the wedge-shaped area $[CED]$ and $[BEA]$ is $\dfrac{\pi}{12}$.

Therefore, the area of the region bounded by line $\overline{CE}$ and arc $\overparen{EC}$ is $$[CEC]=\dfrac{\pi}{6}-\dfrac{\sqrt{3}}{4}$$

We have the area of the region bounded by $\overline{BC}$, arc $\overparen{BE}$ and $\overparen{CE}$ is $$\dfrac{\pi}{6}+(\dfrac{\pi}{6}-\dfrac{\sqrt{3}}{4})=\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{4}$$

And the area of the region bounded by $\overline{CD}$, arc $\overparen{DE}$ and $\overparen{EC}$ (and congruent region on the left side) is $$\dfrac{\pi}{12}-(\dfrac{\pi}{6}-\dfrac{\sqrt{3}}{4})=\dfrac{\sqrt{3}}{4}-\dfrac{\pi}{12}$$

Finally, the area of the region bounded by line $\overline{AD}$, arc $\overparen{AE}$ and $\overparen{DE}$ is $$1-(\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{4})-2\cdot(\dfrac{\sqrt{3}}{4}-\dfrac{\pi}{12})=1-\dfrac{\sqrt{3}}{4}-\dfrac{\pi}{6}$$