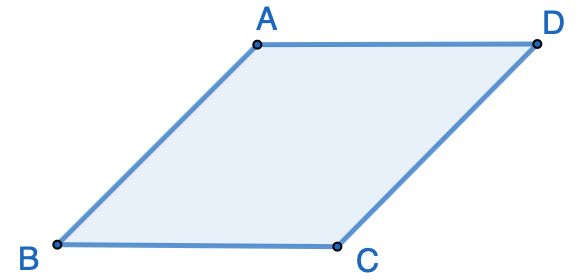
The perimeter of rhombus $ABCD$ is 8 and its area is 2. Find the value of $\angle{ABC}$ in terms of $\pi$. Click here for the solution.
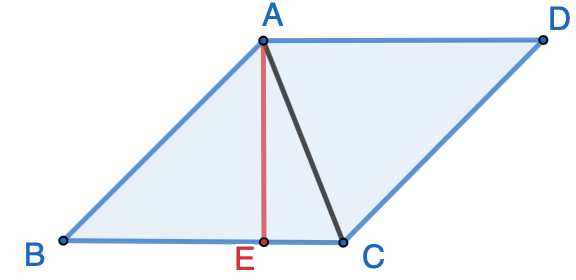
Solution Draw line $AE$ perpendicular to $BC$ with $E$ on $BC$. Connect $A$ and $C$ to form two congruent $\triangle{ABC}$ and $\triangle{ADC}$. Because $ABCD$ is a rhombus, we have
$$ AB=BC=CD=DA=\frac{1}{4} \cdot \text{perimeter of ABCD} =\frac{1}{4}\cdot 8=2$$ $$[\triangle{ABC}]=[\triangle{BCD}]=\frac{1}{2}\cdot[ABCD]=\frac{1}{2}\cdot 2\sqrt{2}=\sqrt{2}$$
$$ \because [\triangle{ABC}]=\frac{1}{2}\cdot BC \cdot AE $$
$$ \therefore AE=2\cdot\frac{[\triangle{ABC}]}{BC}=2\cdot\frac{\sqrt{2}}{2}=\sqrt{2} $$
$$ $$
$$ \because \triangle{ABE}\ \text{is a right triangle} $$
$$ \therefore BE = \sqrt{AB^2-AE^2}=\sqrt{2^2-(\sqrt{2})^2}=\sqrt{2} $$
$$ \because AE = BE, \triangle{ABC}\ \text{is an isosceles right triangle} $$
$$ \therefore \angle{ABC}=45^{\circ}=\frac{\pi}{4} $$