Let $R$, $S$, and $T$ be squares that have vertices at lattice points (i.e., points whose
coordinates are both integers) in the coordinate plane, together with their interiors.
The bottom edge of each square is on the $x$-axis. The left edge $R$ of and the right
edge $S$ of are on the $y$-axis, and $R$ contains as many $\dfrac{9}{4}$ lattice points as does $S$. The top two vertices of $T$ are in $R\cup S$, and $T$ contains $\dfrac{1}{4}$ of the lattice points contained in $R\cup S$. See the figure (not drawn to scale).
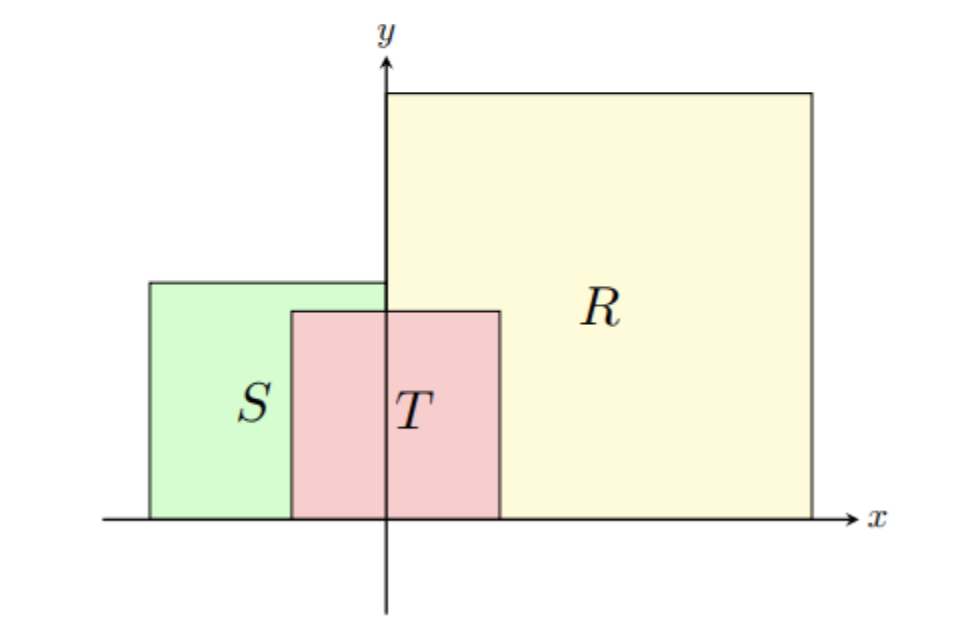
The fraction of lattice points in $S$ that are in $S\cap T$ is 27 times the fraction of lattice
points $R$ in that are in $R\cap T$. What is the minimum possible value of the edge
length of $R$ plus the edge length of $S$ plus the edge length of $T$?
(A) $336$ (B) $337$ (C) $338$ (D) $339$ (E) $340$
Solution: Let $r$, $s$, $t$ be the edge length of square $R$, $S$, and $T$ respectively. Then we have $$(r+1)^2=\dfrac{9}{4}(s+1)^2\ \ \ \ \ (t+1)^2=\dfrac{1}{4}((s+1)^2+(r+1)^2-(s+1))$$ Therefore $$r=\dfrac{3s+1}{2}\ \ \ \ \ t=\dfrac{1}{4}\sqrt{(s+1)(13s+9)}-1$$ Therefore $$r+s+t=\dfrac{3s+1}{2}+s+\dfrac{1}{4}\sqrt{(s+1)(13s+9)}-1$$ $$\approx\dfrac{5}{2}s+\dfrac{\sqrt{13}}{4}s-\dfrac{1}{2}\approx 3.4\cdot s$$
Given that average of the answer choices is around $340$, therefore $s\approx 100$. Since $t$ is an integer, therefore $(s+1)(13s+9)$ must be a perfect square divisible by 16. Plugging in $s=99$, $t=89$ and $s=149$. Therefore $r+s+t=99+89+149=337$. So the answer is $B$.
