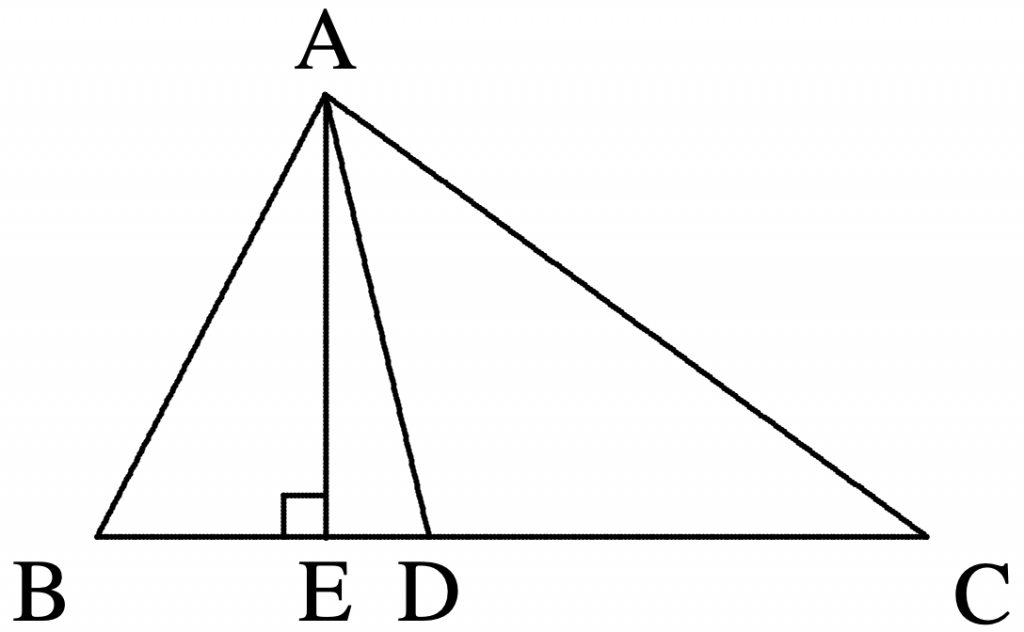
- As shown in the diagram below, in $\triangle{ABC}$, $\angle{B}\gt \angle{C}$, $AD$ is the bisector of the $\angle{BAC}$, $AE\perp BC$ at $E$. Prove that $\angle{DAE}=\dfrac{1}{2}(\angle{B}−\angle{C})$.
2. There are four points $A$, $B$, $C$, $D$ on the plane, such that any three points are not collinear. Prove that in the triangles $ABC$, $ABD$, $ACD$ and $BCD$ there is at least one triangle which has an interior angle not greater than $45^\circ$.
3. In $\triangle{ABC}$, $AB=AC$, $D$, $E$, $F$ are on $AB$, $BC$, $CA$, such that $DE= EF=FD$. Prove that $\angle{DEB}=\dfrac{1}{2}(\angle{ADF}+\angle{CFE})$.
4. In $\angle{ABC}$, $AC=BC$, $\angle{C}=20^\circ$, $M$ is on the side $AC$ and $N$ is on the side $BC$, such that $\angle{BAN}=50^\circ$, $\angle{ABM}=60^\circ$. Find $\angle{NMB}$ in degrees.
