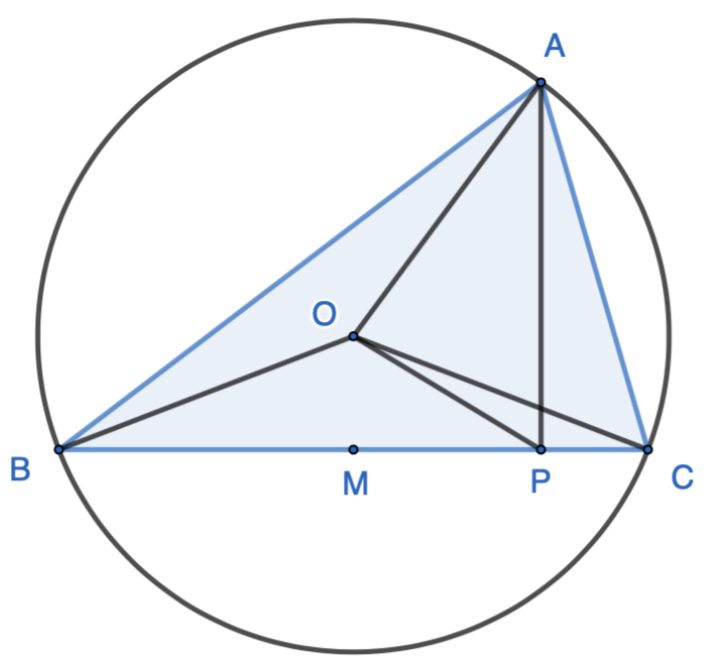
Acute $\triangle{ABC}$ is inscribed inside circle centered at $O$. $P$ is on $BC$ and $AP\perp BC$, and $\angle{ACB}>\angle{ABC}$. Prove the following:
- $\angle{BAC}+\angle{OBC}=90^\circ$
- $\angle{OAP}=\angle{ACB}-\angle{ABC}$
- If $\angle{ACB}-\angle{ABC}\ge 30^\circ$, and $MB=MC$, then $MP\gt CP$
- If $\angle{ACB}-\angle{ABC}\ge 30^\circ$, then $\angle{BAC}+\angle{POC}<90^\circ$
Click here for the solutions.
Proof 1: Because $O$ is the center of the circle, $\triangle{OBC}$ is isosceles. and $\angle{OBC}=\angle{OCB}$. As $\angle{BOC}=2\angle{BAC}$, and $\angle{BOC} +\angle{OBC}+\angle{OCB}=180^\circ$, we have $$2\angle{BAC}+\angle{OBC}+\angle{OBC}=180^\circ$$ Therefore $\boxed{\angle{BAC}+\angle{OBC}=90^\circ}$
Proof 2: Because $O$ is the center of the circle, $\triangle{OAC}$ is isosceles. Therefore $$\angle{OAC}=\dfrac{1}{2}(180^\circ-\angle{AOC})$$ Because $\angle{AOC}=2\angle{ABC}$, we have $$\angle{OAC}=\dfrac{1}{2}(180^\circ-2\angle{ABC})=90^\circ-\angle{ABC}$$ Because $AP\perp BC$, $\triangle{APC}$ is right, $\angle{CAP}=90^\circ-\angle{ACB}$. Therefore $$\angle{OAP}=\angle{OAC}-\angle{CAP}=(90^\circ-\angle{ABC})-(90^\circ-\angle{ACB})=\boxed{\angle{ACB}-\angle{ABC}}$$
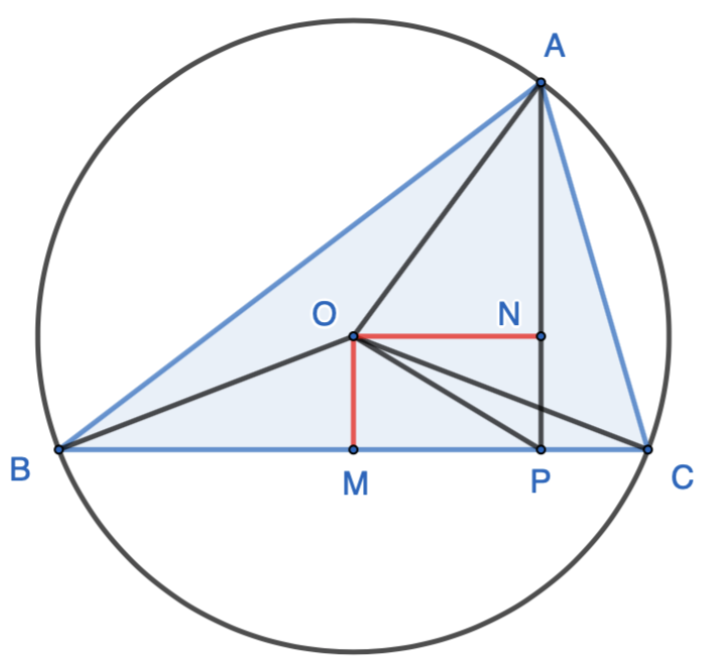
Proof 3: Let $ON\perp AP$ and $OA=OB=OC=r$.
Since $\triangle{AON}$ is right, and $\angle{AOP}=\angle{ACB}-\angle{ABC}\ge 30^\circ$, $$ON=sin(\angle{AOP})\cdot OA\ge sin(30^\circ)\cdot r=\dfrac{r}{2}$$ Since $MB=MC$, and $\triangle{BOC}$ is isosceles, $OM\perp BC$, $OMPN$ is a rectangle. Therefore, $MP=ON\ge \dfrac{r}{2}$.
Since $\triangle{ABC}$ is acute, $O$ is inside $\triangle{ABC}$, and $BC<2r$. Therefore $MB=MC=\dfrac{BC}{2}<r$. Because $MB=MP+CP$, $MP+CP<r$.
Because $MP\ge\dfrac{r}{2}$, $CP<r-MP\le r-\dfrac{r}{2}=\dfrac{r}{2}$. Since $MP\ge\dfrac{r}{2}$, $CP<\dfrac{r}{2}$, $\boxed{MP>CP}$
Proof 4: Since $\triangle{MOP}$ is right, and $OM\perp BC$, $OP>MP>CP$. Therefore $\angle{POC}<\angle{OCB}$.
Since $\angle{BAC}+\angle{OCB}=\angle{BAC}+\angle{OBC}=90^\circ$, Therefore
$$\boxed{\angle{BAC}+\angle{POC}<\angle{BAC}+\angle{OCB}=90^\circ}$$