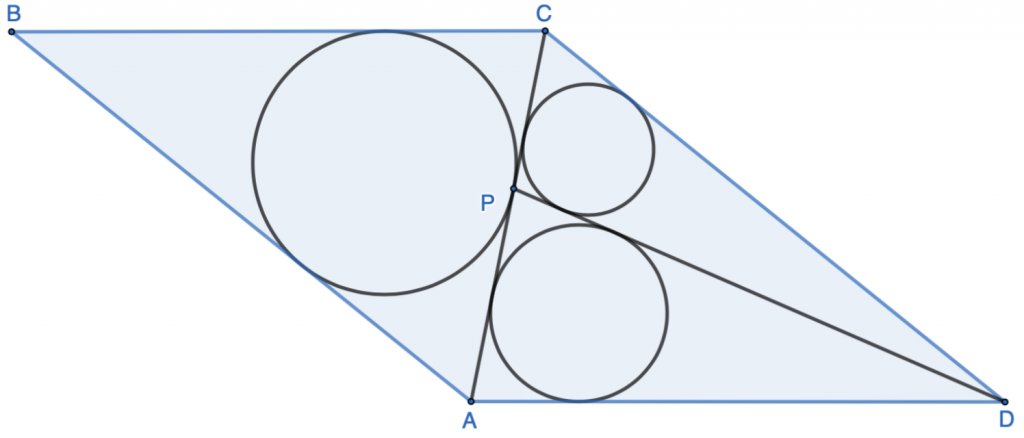
In parallelogram $ABCD$, diagonal $AC$ tangents the incircle of $\triangle{ABC}$ at $P$. Let $r_1$ and $r_2$ be the radii of incircles of $\triangle{ADP}$ and $\triangle{DCP}$ respectively.
1. Prove that $\dfrac{r_1}{r_2}=\dfrac{AP}{CP}$
2. If $AD=PD$, and $\dfrac{AD+CD}{AC}=p$, where $p>1$, prove that $\dfrac{r_1}{r_2}=1+\dfrac{1}{p}$.
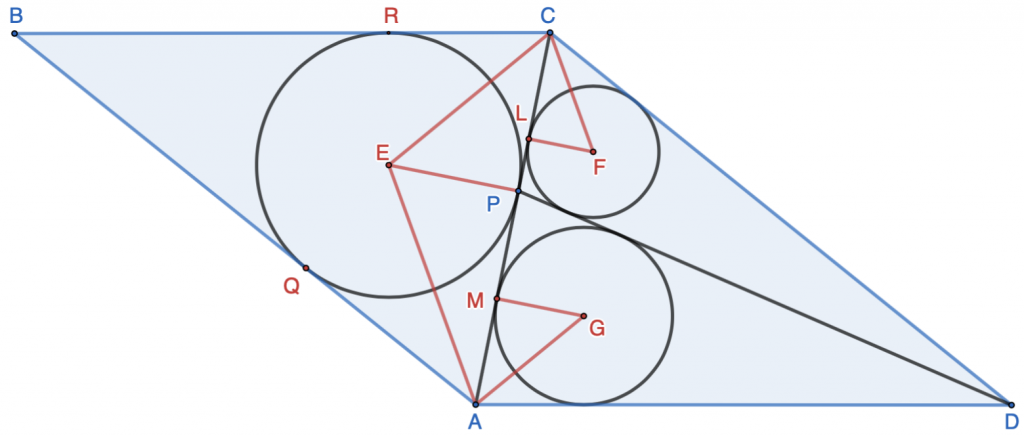
Solution: Draw the digram as shown. Let the incircle centers of $\triangle{ABC}$, $\triangle{DCP}$, and $\triangle{ADP}$ be $E$, $F$, and $G$ respectively.
Draw line $EP$, and $EP\perp AC$, because $AC$ tangents circle $E$ at $P$. Let $AC$ tangent with circle $F$ and $G$ at $L$ and $M$ respectively, so $FL\perp AC$, $GM\perp AC$, and $r_1=GM$, $r_2=FL$. Additionally, let $AB$ and $CB$ tangent with circle $E$ at $Q$ and $R$ respectively.
Draw line $AE$, $AG$, $CE$, $CF$, which are angle bisectors of $\angle{BAC}$, $\angle{CAD}$, $\angle{ACB}$, and $\angle{ACD}$ respectively.
1. Proof: Because $ABCD$ is a parallelogram, we have $AD+AB=CD+BC$. Because $BR$ and $BQ$ tangent circle $E$, $BR=BQ$. Then $AD+AB-BQ=CD+BC-BR$. Because $AB-BQ=AQ$, $BC-BR=CR$, we have $AD+AQ=CD+CR$. Because $AQ$ and $AP$ tangent circle $E$, $AQ=AP$; $CR$ and $CP$ tangent circle $E$, $CR=CP$. Therefore $$AD+AP=CD+CP\tag{1}$$
Because $AM$ tangents circle $G$ at $M$, and $CL$ tangents circle $F$ at $L$, we have $AM=\dfrac{1}{2}{AD+AP-DP}$, $CL=\dfrac{1}{2}{CD+CP-DP}$. Because $AD+AP=CD+CP$, we have $$AM=CL\tag{2}$$
Because $AG$ and $CE$ are the angle bisector of $\angle{CAD}$ and $\angle{ACB}$ respectively, $\angle{CAG}=\dfrac{1}{2}\angle{CAD}$, $\angle{ACE}=\dfrac{1}{2}\angle{ACB}$. Because $ABCD$ is a parallelogram with $AD\parallel BC$, we have $\angle{CAD}=\angle{ACB}$. Therefore $\angle{CAG}=\angle{ACE}$. As $M$ and $P$ is between $A$ and $C$, we have $\angle{MAG}=\angle{PCE}$. Because $M$ and $P$ are tangent points to circle $G$ and $F$ respectively, both $\triangle{MAG}$ and $\triangle{PCE}$ are right triangles. Therefore $\triangle{MAG}\sim \triangle{PCE}$. We have $$\dfrac{GM}{AM}=\dfrac{EP}{CP}\tag{3}$$ Similarly, we have $\triangle{LCF}\sim \triangle{PAG}$, and $$\dfrac{FL}{CL}=\dfrac{EP}{AP}\tag{4}$$ Based on $(2)$, $(3)$, and $(4)$, we have $$\dfrac{GM}{FL}=\dfrac{\dfrac{GM}{AM}}{\dfrac{FL}{CL}}=\dfrac{\dfrac{EP}{CP}}{\dfrac{EP}{AP}}=\dfrac{AP}{CP}$$ Because $r_1=GM$, $r_2=FL$, we have $$\boxed{\dfrac{r_1}{r_2}=\dfrac{AP}{CP}}$$
2. Proof: Let $m=AP$, $n=CP$, $a=AC=m+n$, $b=CD$, $c=AD$, $d=PD$.
Given the assumptions that $AD=PD$, and $\dfrac{AD+CD}{AC}=p$, we have $$c=d\ \ \ \ \ \ \ \tag{5}$$ $$\dfrac{b+c}{m+n}=p\tag{6}$$ Additionally, based on $(1)$, we have $$c+m=b+n\tag{7}$$ Solving $b$ and $c$ in equation $(6)$ and $(7)$, we have $$b=\dfrac{(p+1)m+(p-1)n}{2}\tag{8}$$ $$c=\dfrac{(p-1)m+(p+1)n}{2}\tag{9}$$
According to Stuart’s Theorem, we have $$man+dad=bmb+cnc$$ Substituting $a$, $b$, $c$, $d$ in the above equation, we have $$mn(m+n)+(m+n)(\dfrac{(p-1)m+(p+1)n}{2})^2$$ $$=m(\dfrac{(p+1)m+(p-1)n}{2})^2+n(\dfrac{(p-1)m+(p+1)n}{2})^2$$ Simplifying and factorizing the above equation, we have $$m(m+n)((p+1)n-pm)=0$$ Because $m=AP>0$ and $n=CP>0$, we have $$(p+1)n-pm=0$$ Therefore $$\dfrac{m}{n}=\dfrac{p+1}{p}=1+\dfrac{1}{p}$$ Based on the result of Proof 1, we have $$\boxed{\dfrac{r_1}{r_2}=\dfrac{AP}{CP}=\dfrac{m}{n}=1+\dfrac{1}{p}}$$