It is known that Telsa/SpaceX CEO Elon Musk would ask a job candidate some brain teaser questions during an interview, such as the following:
You’re standing on the surface of the earth. You walk one mile south, one mile west, and one mile north. You end up exactly where you started. Where are you?
Most people will answer that you are at the North Pole, such as in the following, by walking one mile south from the North Pole to point $B$, then, one mile west to point $A$, then one mile north, returning back the North Pole.
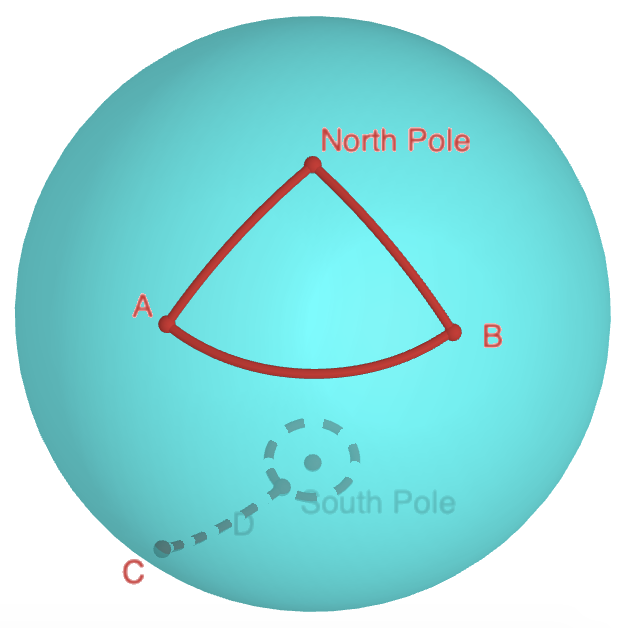
Are there any other places on the earth surface that you could start the walk?
Yes, you may start somewhere near the South Pole. As illustrated below, you start the walk at point $C$, which is one mile south to point $D$, where the circumference of the circle passing $D$ and around the earth axle is exact one mile, then walk one mile west back to point $D$ along the circle, and one mile north, returning back to the starting point $C$.
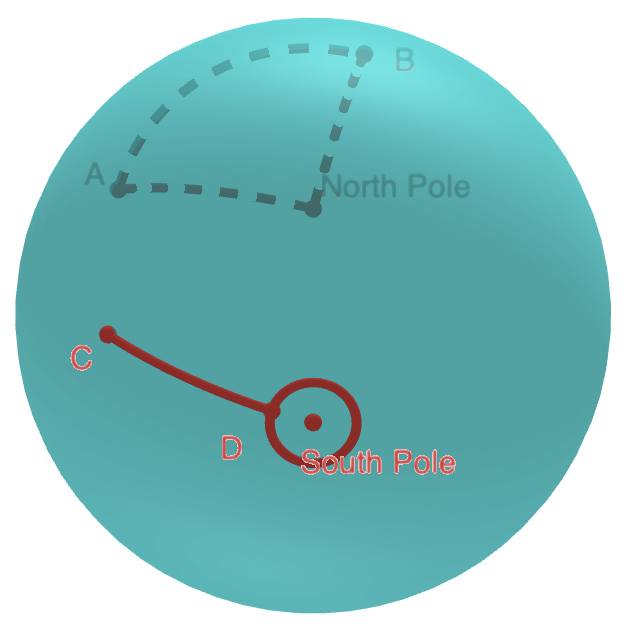
Please note that point $C$ could be anywhere on a circle around the earth axle, with an infinite number of locations. Could you tell if there are additional circles for $C$?
Yes, again 🙂 If the circumference of the circle passing point $D$ is shrink to $\dfrac{1}{n}$ miles, where $n$ is a natural number, and you walk west around the circle $n$ times, the total distance around this circle would be $1$ mile. Therefore, the number of circles passing $C$ is also infinite.
According to his biographer, Elon Musk does not seem to care very much about the correctness of candidates’ answers to his questions. He pays more attentions to how they describe and solve the problems.
Extra: Find the radius of the circle on which point $C$ is located.
Answer: Obviously, the radius $R_n$ must be less than 2 miles, otherwise, point $D$ could not satisfy the constraint. Because the polar region within a 2-mile radius is nearly flat, $R_n \approx 1+\dfrac{1}{2n\pi}$, where $\dfrac{1}{2n\pi}$ is the radius of the circle on which point $D$ is located, and $n$ is a natural number.
When $n=1$, we have $R_1 \approx 1.159155$ miles.
Accurately, you can derive that $$R_n=R\cdot\sin(\dfrac{1}{R}+\sin^{-1}(\dfrac{1}{2n\pi R}))$$ where R is the polar radius of the earth. Assume $R=3950$ miles, and $n=1$, we have a similar result where $R_n\approx 1.159155$ miles.
The similar result is not by accident, as shown in below:
$$R_n=R\cdot\sin(\dfrac{1}{R}+\sin^{-1}(\dfrac{1}{2n\pi R}))$$ $$=R\cdot(\sin(\dfrac{1}{R})\cdot\cos(\sin^{-1}(\dfrac{1}{2n\pi R}))+\cos(\dfrac{1}{R})\cdot\sin(\sin^{-1}(\dfrac{1}{2n\pi R})))$$ $$=R\cdot(\sin(\dfrac{1}{R})\sqrt{1-(\dfrac{1}{2n\pi R})^2}+\cos(\dfrac{1}{R})\cdot \dfrac{1}{2n\pi R})$$
If $R$ is sufficient big, then $$\sin(\dfrac{1}{R})\approx \dfrac{1}{R}\ ,\ \ \ \ \ \sqrt{1-(\dfrac{1}{2n\pi R})^2}\approx 1\ ,\ \ \ \ \ \cos(\dfrac{1}{R})\approx 1$$ Therefore $$R_n\approx R\cdot(\dfrac{1}{R}\cdot 1+1\cdot \dfrac{1}{2n\pi R})=1+\dfrac{1}{2n\pi}$$
Practically it is very hard to walk around the South Pole in a big circle without any ground guidance 🙂 Therefore, you would have to make the circle smaller, but not too small that it makes you loss track and feel dizzy while circling around it 🙂 Say you choose $n=100$, then $R_{100}\approx 1.00159155$ miles. The radius of the circle you walk around $100$ times would be $0.00159155$ miles, which is only about $100.84$ inches. You can draw the circle on the ice around the South Pole with help of a ruler. Then you can pick up any point $1$ mile and $100.84$ inches north of the South Pole to start the journey 🙂
