MATHCOUNTS Exercises – 1

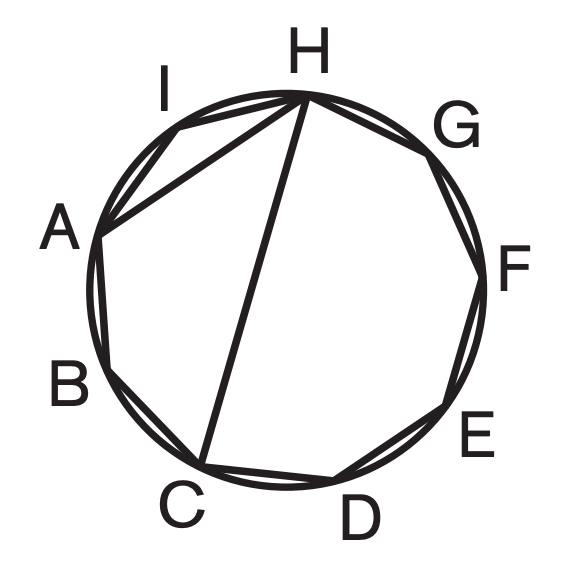
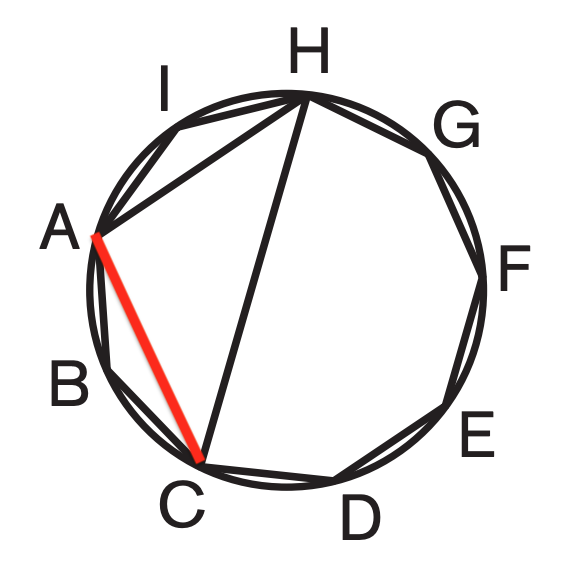
Solution 1 Draw line $\overline{AC}$. $$ \begin{align} &\because\ ABCDEFGHI\ \text{is a regular nonagon} \\ &\therefore \triangle{ABC}, \triangle{AIH}, \triangle{ACH} \text{are isosceles triangle} \\ &\therefore m\angle{HIA}=m\angle{IAB}=m\angle{ABC}=\dfrac{(9-2)\cdot 180^\circ}{9}=140^\circ\\ &\because \triangle{HIA} \cong \triangle{ABC} \\ &\therefore m\angle{IAH}=m\angle{BAC}=\dfrac{180^\circ-m\angle{ABC}}{2}=\dfrac{180^\circ-140^\circ}{2}=20^\circ \\ &\therefore m\angle{CAH}=m\angle{IAB}-m\angle{IAH}-m\angle{BAC}=140^\circ-20^\circ-20^\circ=100^\circ \\ &\therefore m\angle{AHC}=\dfrac{180^\circ-m\angle{CAH}}{2}=\dfrac{180^\circ-100^\circ}{2}=40^\circ \\ \end{align} $$

Solution 2 $$ \begin{align} &\because\ ABCDEFGHI\ \text{is a regular nonagon} \\ &\therefore m\overparen{AB}=m\overparen{BC}=\dfrac{180^\circ}{9}=20^\circ \\ &\therefore m\triangle{AMC}=m\overparen{AB}=m\overparen{BC}=20^\circ+20^\circ=40^\circ \\ \end{align} \\ $$