MATHCOUNTS Exercises – 2

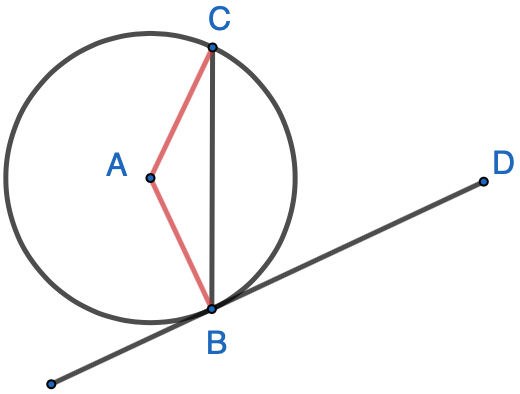
Solution Draw lines $\overline{AB}$ and $\overline{AC}$ $$\begin{align} &\because major\ \overparen{BC\ }=230^\circ \\ &\therefore minor\ \overparen{BC\ }=360^\circ-major\ \overparen{BC\ }=360^\circ-230^\circ=130^\circ \\ &\therefore m\angle{BAC}=minor\ \overparen{BC\ }=130^\circ \\ &\because\ \overline{AB} = \overline{AC} \\ &\therefore \triangle{ABC}\ is\ isosceles \\ &\therefore m\angle{ABC}=m\angle{ACB}=\dfrac{180^\circ-m\angle{BAC}}{2}=\dfrac{180^\circ-130^\circ}{2}=25^\circ \\ &\because\ \overleftrightarrow{BD}\ is\ tangent\ to\ circle\ A\ at\ B \\ &\therefore\ \overline{AB} \perp \overleftrightarrow{BD} \\ &\therefore m\angle{ABD}=90^\circ \\ &\therefore m\angle{ABC}+m\angle{CBD}=m\angle{ABD}=90^\circ \\ &\therefore m\angle{CBD}=90^\circ-m\angle{ABC}=90^\circ-25^\circ=65^\circ \blacksquare \\ \end{align} $$