Given an equilateral $\triangle{ABC}$ shown below, $AB=BC=CA=1$, point $D$ and $E$ trisect side $AB$, point $F$ and $G$ trisect side $BC$, point $H$ and $I$ trisect side $CA$. Two overlapping equilateral triangles are formed by linking various intersect points. Find the ratio of the star-shaped area covered by the overlapping equilateral triangles to the area of $\triangle{ABC}$. Click here for the solutions.
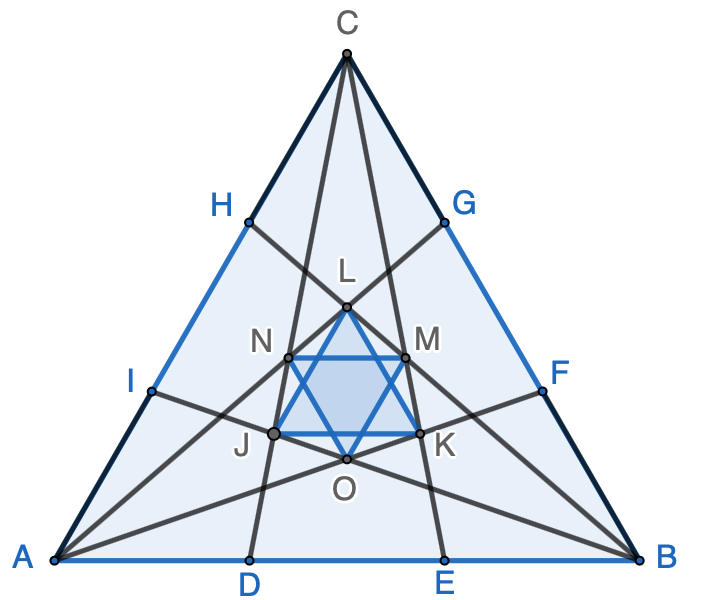
Solution 1 – Use Mass Points Because point $D$ and $E$ trisect side $AB$, point $F$ and $G$ trisect side $BC$, we can have the following balanced mass:
$$ A_{mass}=2, B_{mass}=1, D_{mass}=A_{mass}+B_{mass}=3$$ $$C_{mass}=1, I_{mass}=A_{mass}+C_{mass}=3$$ $$ J_{mass}=C_{mass}+D_{mass}=B_{mass}+I_{mass}=4$$
Therefore
$$\frac{CJ}{CD}=\frac{D_{mass}}{J_{mass}}=\frac{3}{4}$$
Because $ JK \parallel DE $, we have $\triangle{CJK} \sim \triangle{CDE}$.
Therefore $$\frac{JK}{DE}=\frac{CJ}{CD}=\frac{3}{4}$$
Because point $D$ and $E$ trisect side $AB$, we have $$DE=\frac{3}{4}\cdot DE=\frac{3}{4}\cdot \frac{1}{3}=\frac{1}{4} \tag{1}$$
Because point $D$ and $E$ trisect side $AB$, point $F$ and $G$ trisect side $BC$, we can have the following balanced mass: $$A_{mass}=2, B_{mass}=1, D_{mass}=A_{mass}+B_{mass}=3$$ $$C_{mass}=2, G_{mass}=B_{mass}+C_{mass}=3$$ $$ N_{mass}=C_{mass}+D_{mass}=A_{mass}+G_{mass}=5$$
Therefore $$\frac{CN}{CD}=\frac{D_{mass}}{N_{mass}}=\frac{3}{5}$$ Because $ NM \parallel DE $, we have $\triangle{CNM} \sim \triangle{CDE}$. Therefore $$\frac{NM}{DE}=\frac{NM}{CD}=\frac{3}{5}$$ Because point $D$ and $E$ trisect side $AB$, we have $$NM=\frac{3}{5}\cdot DE=\frac{3}{5}\cdot \frac{1}{3}=\frac{1}{5} \tag{2}$$ Therefore, the side length of equilateral $\triangle{JKL}$ is $\dfrac{1}{4}$ and the side length of equilateral $\triangle{MNO}$ is $\dfrac{1}{5}$. Let’s take a closer look at the two triangles as the following: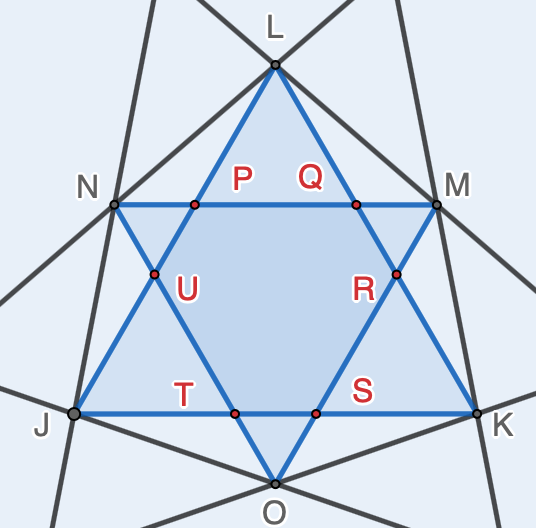
Let $PQ=x$, $NP=y$, we have the following: $$ \begin{array}{rcrcr}
x & + & 2y & = & \frac{1}{5} \\
2x & + & y & = & \frac{1}{4}
\end{array} $$
Solve the above linear equations, we have $x = \dfrac{1}{10}$, $y=\dfrac{1}{20}$. Therefore, the area covered by $\triangle{JKL}$ and $\triangle{MNO}$ is $$[\triangle{MNO}] + 3\cdot [\triangle{LPQ}] = \frac{1}{4}(\frac{1}{5})^2\cdot\sqrt{3} + 3\cdot \frac{1}{4}\cdot (\frac{1}{10})^2 \cdot \sqrt{3} = \frac{7}{400}\sqrt{3}$$ Therefore, the answer to the question is $$\frac{\frac{7}{400}\sqrt{3}}{[\triangle{ABC}]}=\frac{\frac{7}{400}\sqrt{3}}{\frac{\sqrt{3}}{4}}=\frac{7}{100}$$
Solution 2 – Use Menelaus’s Theorem Consider $\triangle{ACD}$ and $\triangle{ABI}$, apply Menelaus’s theorem, we have $$\frac{AB}{BD}\cdot\frac{DJ}{JC}\cdot\frac{DI}{DA}=1$$ Because point $D$ and $E$ trisect side $AB$, point $H$ and $I$ trisect side $CA$, and $AB=BC=CA=1$, we have $$\frac{1}{\frac{2}{3}}\cdot\frac{DJ}{JC}\cdot\frac{\frac{2}{3}}{\frac{1}{3}}=1$$ We have $$\frac{DJ}{JC}=\frac{1}{3}$$ Therefore $$\frac{CJ}{CD}=\frac{3}{4}$$
Similarly, consider $\triangle{BCD}$ and $\triangle{ABG}$, we have $$\frac{BA}{AD}\cdot\frac{DN}{NA}\cdot\frac{CG}{GB}=1$$ Because point $D$ and $E$ trisect side $AB$, point $F$ and $G$ trisect side $BC$, and $AB=BC=CA=1$, we have $$\frac{1}{\frac{1}{3}}\cdot\frac{DN}{NC}\cdot\frac{\frac{1}{3}}{\frac{2}{3}}=1$$ We have $$\frac{DN}{NC}=\frac{2}{3}$$ Therefore $$\frac{CN}{CD}=\frac{3}{5}$$ From here, we can calculate the length of $JK$ and $NM$ and follow the same steps in Solution 1 to obtain the same answer.