MathFun4Kids

Crazy Jumping Frog

Posted on January 29, 2020 by kevin

Crazy Jumping Frog can jump forward at a distance either 1 foot or 2 feet. The probability it jumps 1 foot forward is $p$, and the probability it jumps 2 feet is $1-p$. Assume that each jump is independent and the frog has infinite amount of energy 🙂

What the expected distance after the frog making $n$ jumps?
If there is an uncovered well $n$ feet away from the frog, what is the probability that the frog fells into the well if it jumps forward trying to pass the well?

Click here for the solutions.

Posted in Algebra, Probability | Comments Off

MATHCOUNTS Exercises – 17

Posted on January 28, 2020 by kevin

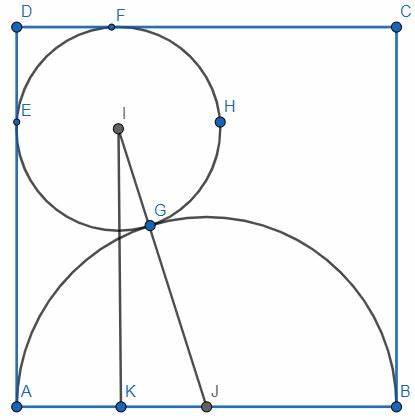
In rectangle $ABCD$, shown here, point $M$ is the midpoint of side $BC$, and point $N$ lies on $CD$ such that $DN:NC=1:4$. Segment $BN$ intersects $AM$ and $AC$ at points $R$ and $S$, respectively. If $NS:SR:RB=x:y:z$, where $x$, $y$ and $z$ are positive integers, what is the minimum possible value of $x + y + z$? Source: MATHCOUNTS 2012 State Sprint Round. Click here for solutions.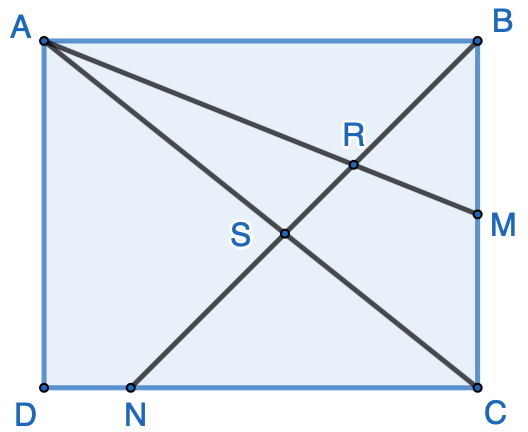

Solution 1 – Using Similar Triangles Please visit Art of Problem Solving for using Similar Triangles and Proportional Reasoning to solve the problem.

Solution 2 – Using Mass Points This may be the simplest method found without drawing extra lines.

$$ \because DN:NC=1:4 $$ $$ \therefore CN:AB=CN:CD=NC:(DN+NC)=4:(1+4)=4:5$$ $$ \because AB \parallel CD \ \ \ and \ \ \angle{ASB}=\angle{CSN} $$ $$ \therefore \triangle{ASB} \sim \triangle{CSN}$$ $$ \therefore NS:BS=CS:AS=CN:AB=4:5\tag{1}$$ For $\triangle{ABC}$, let $A_{mass}=4$, $C_{mass}=5$, then, $$S_{mass}=A_{mass}+C_{mass}=4+5=9$$ Because $M$ is the midpoint of $BC$, $B_{mass}=C_{mass}=5$, and $$M_{mass}=B_{mass}+C_{mass}=5+5=10$$ Finally, we have balanced mass at $S$: $$S_{mass}=A_{mass}+M_{mass}=B_{mass}+S_{mass}=14$$ 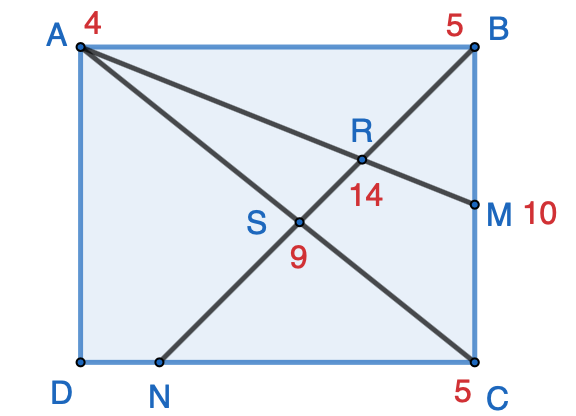Therefore $$RB:BS=9:14\tag{2}$$ $$SR:BS=5:14\tag{3}$$ Combine (1), (2) and (3), we have: $$NS:SR:RB=(NS:BS):(SR:BS):(RB:BS)=(4:5):(5:14):(9:14)$$ $$= (56:70):(25:70):(45:70)=56:25:45=x:y:z$$ Therefore, $x+y+z=56+25+45=126$

Solution 3 – Using Crossed Ladders Theorem Draw line $RT$ parallel to $AB$ and intersecting $BC$ at $T$, and line $ME$ parallel to $AB$ and intersecting $BN$ at $E$.
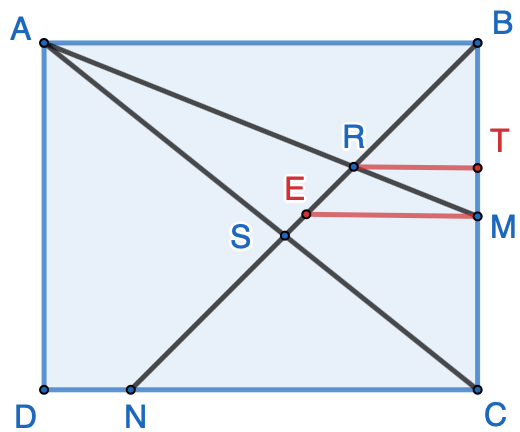$$ \because DN:NC=1:4 $$ $$ \therefore AB:CN=CD:CN=(DN+NC):NC=(1+4):4=5:4 \tag{1}$$ $$ \because AB \parallel CD \ \ \ and \ \ \angle{ASB}=\angle{CSN} $$ $$ \therefore \triangle{ASB} \sim \triangle{CSN}$$ $$ \therefore BS:NS=AB:CN=5:4$$ $$BS:BN=BS:(BS+NS)=5:(4:5)=5:9 \tag{2}$$ Applying Crossed ladders theorem, we have $$ \because RT \parallel AB \parallel EM \parallel CD $$ $$ \therefore \frac{1}{RT}=\frac{1}{AB}+\frac{1}{EM}\tag{3}$$ Additionally $$ \because ME \parallel CN $$ $$ \therefore \triangle{BME}\sim\triangle{BCD} $$ Because point $M$ is the midpoint of side $BC$, therefore $$EM:NC=BM:BC=1:2$$ Apply (1), we have $$EM=\frac{1}{2}NC=\frac{1}{2}\cdot\frac{4}{5}AB=\frac{2}{5}AB\tag{4} $$ Apply (4) to (3), we have $$ \frac{1}{RT}=\frac{1}{AB}+\frac{1}{\frac{2}{5}AB}=\frac{7}{2}\cdot\frac{1}{AB}$$ $$\therefore RT:AB=2:7$$ Apply (1), we have $$RT:NC=(RT:AB) \cdot (AB:CN) = (2:7)\cdot(5:4)=5:14$$ $$ \because \triangle{BTR} \sim \triangle{BCN} $$ $$\therefore RB:NB=RT:NC=5:14\tag{5}$$ $$\therefore SR:NB=(BS-RB):NB = BS:NB-RB:NB=\frac{5}{9}-\frac{5}{14}=\frac{25}{126}\tag{6}$$ Additionally, $$NS:NB=NS:(NS+SR)=4:(4+5)=4:9\tag{7}$$ Combine (5), (6) and (7), we have: $$NS:SR:RB=(4:9):(25:126):(5:14)=56:25:45=x:y:z$$ Therefore, we reach the same answer: $x+y+z=56+25+45=126$

Posted in Geometry, MATHCOUNTS | Comments Off

MATHCOUNTS Exercises – 16

Posted on January 26, 2020 by kevin

A semicircle and a circle are placed inside a square with sides of length 4 cm as shown. The circle is tangent to two adjacent sides of the square and to the semicircle. The diameter of the semicircle is a side of the square. In centimeters, what is the radius of the circle?Source: MATHCOUNTS 2012 State Target Round. Click here for the solution.

Solution First, connect the center of the circle with the center of the semicircle. Then drop a perpendicular from the center of the circle to side AB, as shown.

Let $r$ be the radius of the circle. So, segment $IJ=2+r$, since the side of square $ABCD$ is 4. Also, segment $IK=4-r$ and $KJ=2-r$. Since $IK \perp KJ$, we can set up a Pythagorean:
$$(4-r)^2+(2-r)^2=(2+r)^2$$
This simplifies to $$16-8r+r^2+4-4r+r^2=4+4r+r^2$$ Simplifying further, we get a quadratic equation:
$$r^2-16r+16=0$$
Applying the quadratic formula, we get $r=8-4\sqrt{3}$.

Posted in Circles in a Square, Geometry, MATHCOUNTS | Comments Off

MATHCOUNTS Exercises – 15

Posted on January 22, 2020 by kevin

How many distinct unit cubes are there with two faces painted red, two faces painted green and two faces painted blue? Two unit cubes are considered distinct if one unit cube cannot be obtained by rotating the other. SOURCE: 2014 MATHCOUNTS Chapter Target Round. Click here for the solution.

Solution First, there is only one way to paint the cube with all opposite faces painted in the same color, as shown below, with the front face colored in red:

Second, there are 3 ways to paint the cube with one pair of opposite faces in the same color, while the other two pairs of opposite faces in different colors, as shown below, with the front face in the same color of the back face:

Finally, there are 2 ways to paint the cube without any pair of opposite faces in the same color, as shown below, with the front face colored in red:

Therefore, the final answer to the question is 6.

Posted in Combinatorics, Geometry, MATHCOUNTS | Comments Off

MATHCOUNTS Exercises – 14

Posted on January 19, 2020 by kevin

Lisa wants to use her calculator to square a two-digit positive integer, but she accidentally enters the tens digit incorrectly. When she squares the number entered, the result is 2340 greater than the result she would have gotten had she correctly entered the tens digit. What is the sum of the two-digit number Lisa entered and the two-digit number she meant to enter? Source: 2019 MATHCOUNTS Chapter Sprint Round. Click here for the solution.

Solution Lets assume the bigger 2-digit number is $10x+y$, and the smaller 2-digit number is $10z+y$, we have: $$(10x + y)^2-(10z+y)^2=2340$$ $$100x^2+20xy+y^2-(100z^2+20zy+y^2)=2340$$ Simplify the above equation, we have: $$(x-z)(5x+y+5z)=117=1\cdot 3\cdot 3\cdot 13$$ $$ \because 10 > x > z > 0 $$ $$\therefore x-z=1 \ \ or \ \ x-z=3 $$ If $x-z=1$, we have $$ 5x + y + 5z=117 $$ which is impossible, as the maximum possible value of $5x+y+5z$ is 99. Therefore, $$x-z=3\tag{1}$$ $$5x+y+5z=39\tag{2}$$ From (1), we have $$x=z+3\tag{3}$$ Based on (2) and (3), we have $$5(z+3)+y+5z=39$$ Simplify the above equation, we have $$y+10z=24$$ Since $y$ and $z$ are single digit numbers, the only solution is $$ y=4 \ \ \ and \ \ \ z=2$$ Therefore $x=5$. The sum of $10x+y$ and $10z+y$ is $$ 54+24=78$$

Posted in Algebra, MATHCOUNTS | Comments Off

Crazy Jumping Frog

MATHCOUNTS Exercises – 17

MATHCOUNTS Exercises – 16

MATHCOUNTS Exercises – 15

MATHCOUNTS Exercises – 14

Archives

Meta

Categories