$O$ is an interior point of regular hexgon $ABCDEF$.
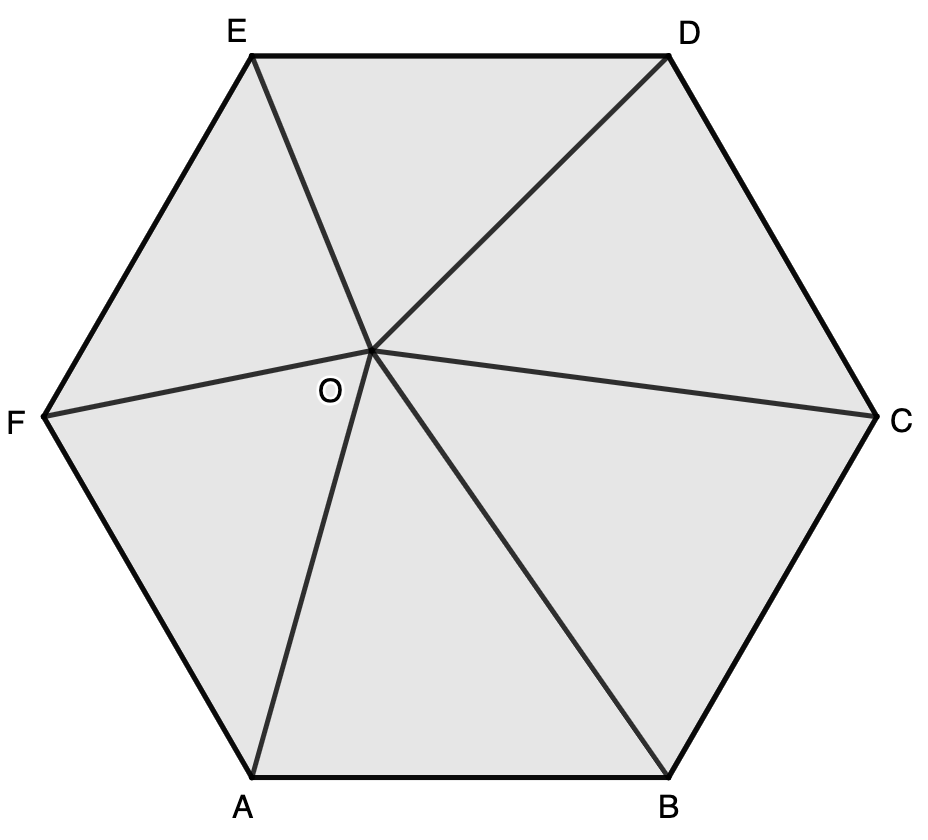
Prove that $[\triangle{OEF}]=2[\triangle{OAB}]+2[\triangle{OCD}]-3[\triangle{OBC}]$
Click here for the proof.
Proof 1: Without loss of generality, assume that $ABCDEF$ is unit regular hexgon with its center at $(0,0)$, $A$ at $(-\dfrac{1}{2},-\dfrac{\sqrt{3}}{2})$, $B$ at $(\dfrac{1}{2},-\dfrac{\sqrt{3}}{2})$, $C$ at $(1,0)$, etc. Then the liner equations for line $AB$, $BC$, $CD$, and $EF$ are:
$y+\dfrac{\sqrt{3}}{2}=0$
$\sqrt{3}x-y-\sqrt{3}=0$
$\sqrt{3}x+y-\sqrt{3}=0$
$\sqrt{3}x-y+\sqrt{3}=0$
Let $O$ at $(a, b)$. Denote $O(XY)$ as the distance from $O$ to line $XY$. The distances from $O$ to $AB$, $BC$, $CD$ and $EF$ are:
$O(AB)=\dfrac{\sqrt{3}}{2}+b$
$O(BC)=-\dfrac{\sqrt{3}a-b-\sqrt{3}}{\sqrt{(\sqrt{3})^2+1^2}}=\dfrac{b+(1-a)\sqrt{3}}{2}$
$O(CD)=-\dfrac{\sqrt{3}a+b-\sqrt{3}}{\sqrt{(\sqrt{3})^2+1^2}}=\dfrac{(1-a)\sqrt{3}-b}{2}$
$O(EF)=\dfrac{\sqrt{3}a-b+\sqrt{3}}{\sqrt{(\sqrt{3})^2+1^2}}=\dfrac{(1+a)\sqrt{3}-b}{2}$
Therefore: $2\cdot O(AB)+2\cdot O(CD)-3\cdot O(BC)$
$=2\cdot(\dfrac{\sqrt{3}}{2}+b)+2\cdot\dfrac{(1-a)\sqrt{3}-b}{2}-3\cdot\dfrac{b+(1-a)\sqrt{3}}{2}=\dfrac{(1+a)\sqrt{3}-b}{2}=O(EF)$
which implies $[\triangle{OEF}]=2[\triangle{OAB}]+2[\triangle{OCD}]-3[\triangle{OBC}]$.
Proof 2: Without loss of generality, assume that $ABCDEF$ is unit regular hexgon.
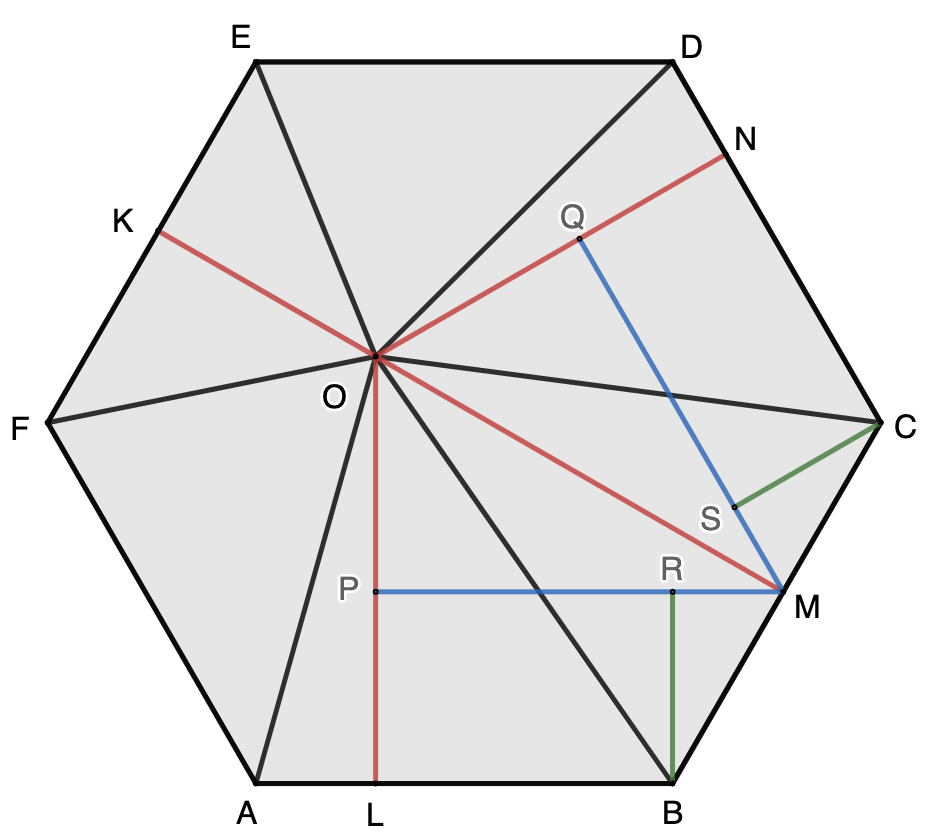
Let point $K$, $L$, $M$, and $N$ on $EF$, $AB$, $BC$, and $CD$ respectively so that $OK\perp EF$, $OL\perp AB$, $OM\perp BC$, and $ON\perp CD$.
Let point $P$ and $Q$ on $OL$ and $ON$ respectively so that $MP\perp OL$ and $MQ\perp ON$.
Let point $R$ and $S$ on $MP$ and $MQ$ respectively so that $BR\perp MP$ and $CS\perp MQ$. Therefore both $BLPR$ and $CNQS$ are rectangles.
$\angle{LOM}=540^\circ-\angle{OLB}-\angle{OMB}-\angle{ABC}=360^\circ-90^\circ-90^\circ-120^\circ=60^\circ$
Therefore, $OP=\dfrac{1}{2}OM$ and $PL=OL-OP=OL-\dfrac{1}{2}OM$.
Because $MP\perp OL$, $OL\perp AB$, we have $MP\parallel AB$, and
$\angle{RMB}=180^\circ-\angle{ABC}=180^\circ-120^\circ=60^\circ$
Therefore
$MB=\dfrac{2}{\sqrt{3}}RB=\dfrac{2\sqrt{3}}{2}PL=\dfrac{2\sqrt{3}}{2}(OL-\dfrac{1}{2}OM)$
Similarly, we have
$MC=\dfrac{2\sqrt{3}}{3}(ON-\dfrac{1}{2}OM)$
Because $MB+MC=BC=1$, we have $$\dfrac{2\sqrt{3}}{3}(OL-\dfrac{1}{2}OM)+\dfrac{2\sqrt{3}}{3}(ON-\dfrac{1}{2}OM)=1\tag{1}$$
Simplifying $(1)$, we have $$OL+ON-OM=\dfrac{\sqrt{3}}{2} \tag{2}$$
Because $BC\parallel EF$, $OK\perp EF$ and $OM\perp BC$, $M$, $O$ and $M$ are co-linear and $$OK+OM=KM=\sqrt{3}$$
Applying $(2)$, We have $$OK=\sqrt{3}-OM=2(OL+ON-OM)-OM=2\cdot OL+2\cdot ON-3\cdot OM$$
which implies $[\triangle{OEF}]=2[\triangle{OAB}]+2[\triangle{OCD}]-3[\triangle{OBC}]$.
Proof 3: Without loss of generality, assume that $ABCDEF$ is unit regular hexgon.
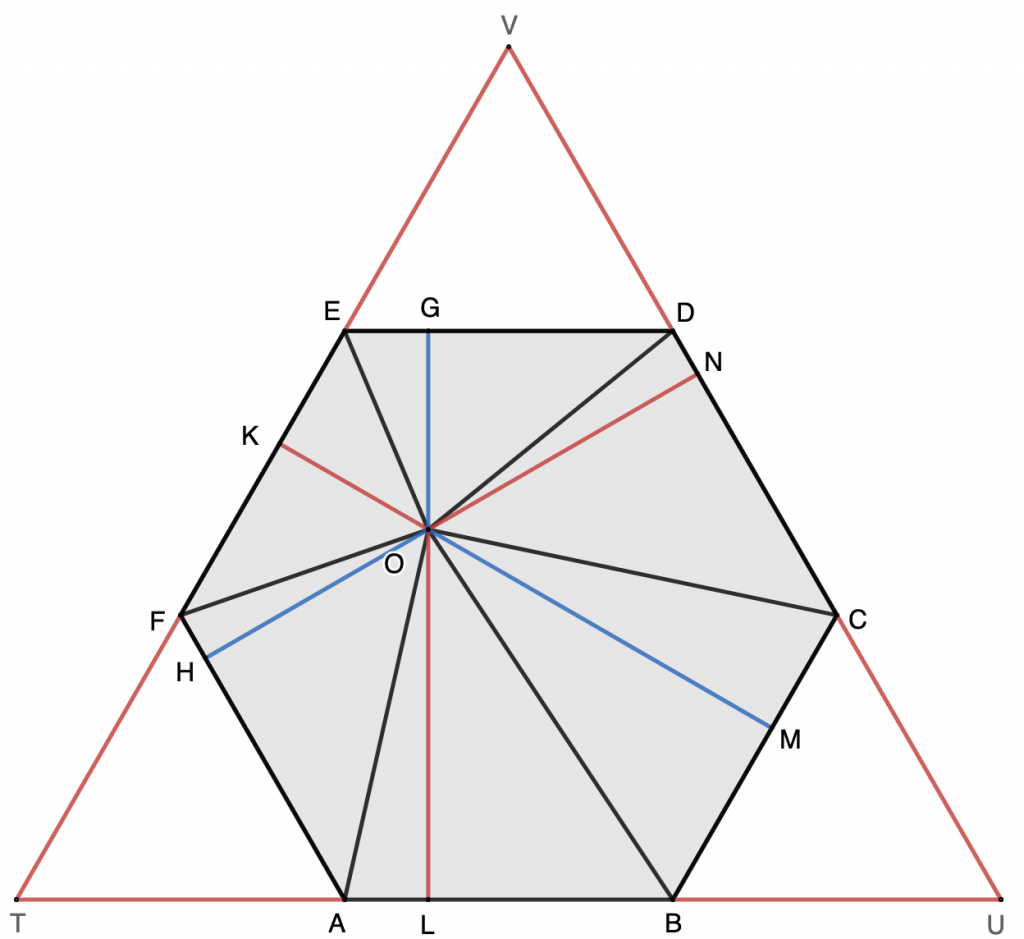
Let $GL$ pass $O$ and $GL\perp AB$, $KM$ pass $O$ and $KM\perp BC$, $HN$ pass $O$ and $HN\perp CD$. As $ABCDEF$ is a regular hexgon, $AB\parallel DE$, $BC\parallel EF$, and $CD\parallel FA$. Therefore $GL\perp DE$, $KM\perp EF$, and $HN\perp FA$.
Extend $AB$, $CD$, and $EF$ to form equilateral $\triangle{TUV}$, with its side length as $3$. Because $OK\perp VT$, $OL\perp TU$, and $ON\perp UV$, we have $$OK+OL+ON=\dfrac{3\sqrt{3}}{2}\tag{1}$$
as $OK$, $OL$ and $ON$ are heights of $\triangle{OEF}$, $\triangle{OAB}$ and $\triangle{OCD}$ respectively and their sum is equal to the height of equilateral $\triangle{TUV}$. Similarly, $$OG+OH+OM=\dfrac{3\sqrt{3}}{2}\tag{2}$$
Additionally, $$OK+OM=\sqrt{3}\tag{3}$$ $$OG+OL=\sqrt{3}\tag{4}$$ $$ OH+ON=\sqrt{3}\tag{5}$$
Subtracting both side $(3)$ from $(1)$, we have $$OL+ON-OM=\dfrac{\sqrt{3}}{2}\tag{6}$$
Because $(3)$ and $(6)$, we have $$OK=\sqrt{3}-OM=2\cdot(OL+ON-OM)-OM=2\cdot OL+2\cdot ON-3\cdot OM$$
which implies $[\triangle{OEF}]=2[\triangle{OAB}]+2[\triangle{OCD}]-3[\triangle{OBC}]$.
Proof 4: Extend $AB$, $CD$, and $EF$ to form equilateral $\triangle{TUV}$, with its side length $3\cdot AB$.
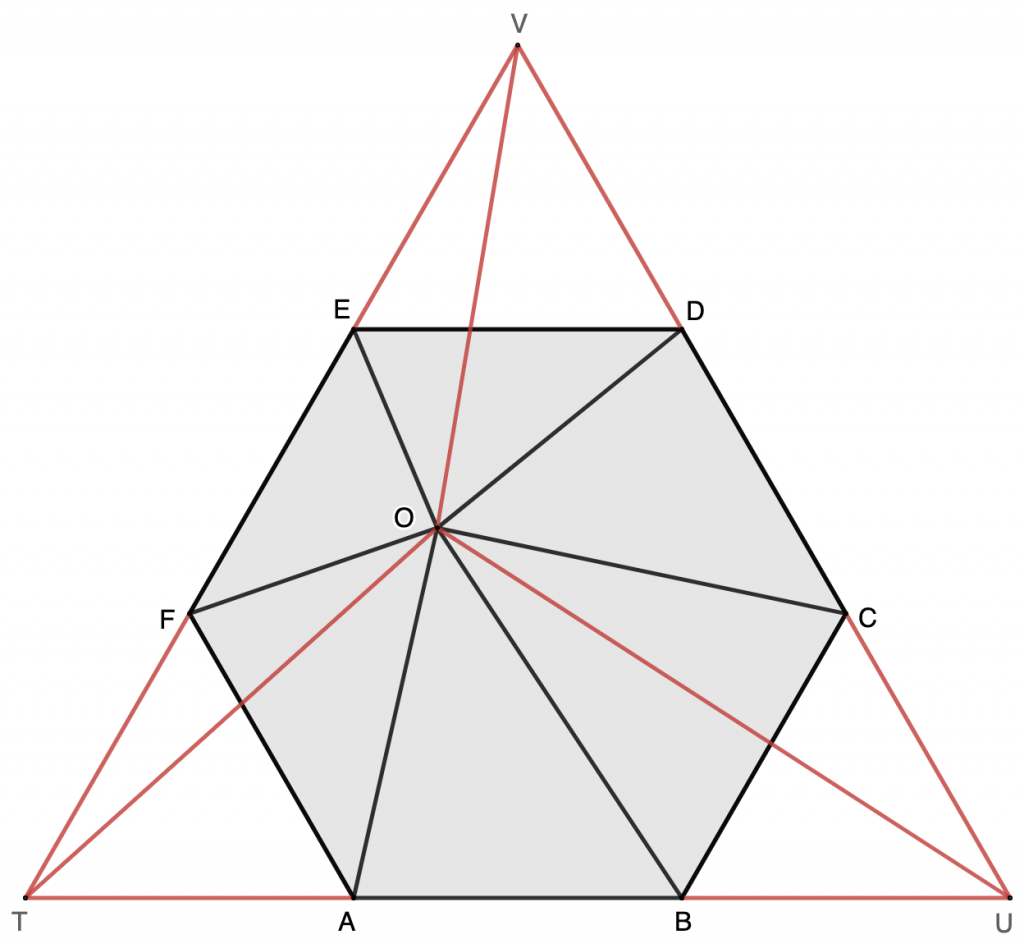
Draw line $OT$, $OU$, and $OV$. Therefore:
$[\triangle{OTU}]=[\triangle{OTA}]+[\triangle{OAB}]+[\triangle{OBU}]=3[\triangle{OAB}]$
$[\triangle{OUV}]=[\triangle{OUC}]+[\triangle{OCD}]+[\triangle{ODV}]=3[\triangle{OCD}]$
$[\triangle{OVT}]=[\triangle{OVE}]+[\triangle{OEF}]+[\triangle{OFT}]=3[\triangle{OEF}]$
Let the $[\triangle{FTA}=\triangle{BUC}=\triangle{DVE}=S$. The area of hexgon $ABCDEF$ is $6S$, and $[\triangle{TUV}]=9S$. Therefore
$$[\triangle{OTU}]+[\triangle{OUV}]+[\triangle{OVT}]=9S$$
$$3[\triangle{OAB}]+3[\triangle{OCD}]+3[\triangle{OEF}]=9S$$
$$[\triangle{OAB}]+[\triangle{OCD}]+[\triangle{OEF}]=3S\tag{1}$$
Because $BC\parallel EF$, therefore $$[\triangle{OBC}]+[\triangle{OEF}]=2S\tag{2}$$
Replace $S$ in $(1)$ with $(2)$, we have:
$$2([\triangle{OAB}]+[\triangle{OCD}]+[\triangle{OEF}])=3([\triangle{OBC}]+[\triangle{OEF}])$$
We have $[\triangle{OEF}]=2[\triangle{OAB}]+2[\triangle{OCD}]-3[\triangle{OBC}]$.
