In $\triangle{ABC}$, $D$ is a point on $BC$. $\angle{ABC}=100^\circ$, $\angle{BCA}=20^\circ$, $\angle{BAD}=50^\circ$. Prove $AB=CD$.
Click here for the proof.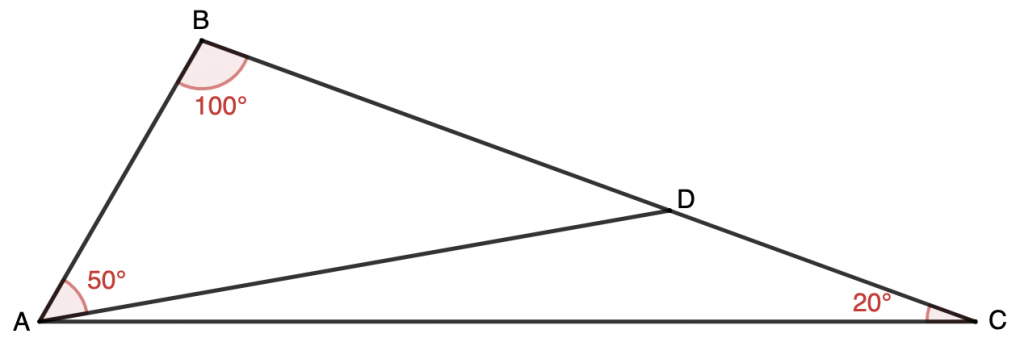
Proof 1: Clearly, $\angle{ADC}=150^\circ$, and $\angle{CAD}=10^\circ$. According to the law of sines, we have:
$ \dfrac{sin\angle{BCA}}{AB}=\dfrac{sin\angle{ABC}}{AC}$ and $ \dfrac{sin\angle{CAD}}{CD}=\dfrac{sin\angle{ADC}}{AC}$
Therefore
$AB=\dfrac{sin\angle{BCA}}{sin\angle{ABC}}AC=\dfrac{sin(20^\circ)}{sin(100^\circ)}AC=\dfrac{2sin(10^\circ)cos(10^\circ)}{sin(80^\circ)}AC=\dfrac{2sin(10^\circ)cos(10^\circ)}{cos(10^\circ)}AC$
$$=2sin(10^\circ)AC$$
$CD=\dfrac{sin\angle{CAD}}{sin\angle{ADC}}AC=\dfrac{sin(10^\circ)}{sin(150^\circ)}AC=\dfrac{sin(10^\circ)}{sin(30^\circ)}AC=\dfrac{sin(10^\circ)}{\dfrac{1}{2}}AC=2sin(10^\circ)AC$
We have $\boxed{AB=CD}$.
Proof 2: Clearly, $\angle{BDA}=30^\circ$, and $\angle{BAC}=60^\circ$. According to the law of sines, we have:
$ \dfrac{sin\angle{BDA}}{AB}=\dfrac{sin\angle{BAD}}{BD}$ and $ \dfrac{sin\angle{BCA}}{AB}=\dfrac{sin\angle{BAC}}{BC}$
Therefore
$BD=\dfrac{sin\angle{BAD}}{sin\angle{BDA}}AB=\dfrac{sin(50^\circ)}{sin(30^\circ)}AB=\dfrac{sin(50^\circ)}{\dfrac{1}{2}}AB=2cos(40^\circ)AB$
And
$BC=\dfrac{sin\angle{BAC}}{sin\angle{BCA}}AB=\dfrac{sin(60^\circ)}{sin(20^\circ)}AB=\dfrac{sin(60^\circ+20^\circ)}{sin(20^\circ)}AB$
$=\dfrac{cos(40^\circ)sin(20^\circ)+sin(40^\circ)cos(20^\circ)}{sin(20^\circ)}AB$
$=\dfrac{cos(40^\circ)sin(20^\circ)+2sin(20^\circ)cos(20^\circ)cos(20^\circ)}{sin(20^\circ)}AB$$
$=(cos(40^\circ)+2cos^2(20^\circ))AB=(cos(40^\circ)+cos(40^\circ)+1)AB$
$=(2cos(40^\circ)+1)AB$
Therefore $$CD=BC-BD=(2cos(40^\circ)+1)AB-2cos(40^\circ)AB=AB$$
Proof 3: Let $E$ be on $AC$ so that $AB=AE$.
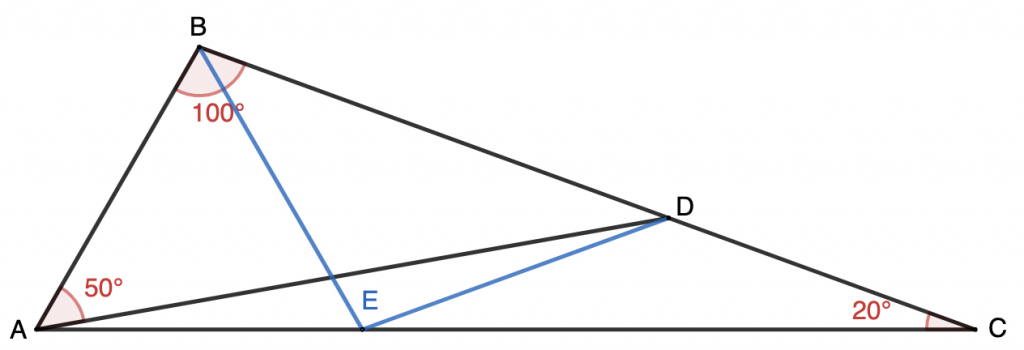
As $\angle{BAE}=60^\circ$, $\triangle{ABE}$ is equilateral. Therefore $\angle{AEB}=60^\circ$
Because $\angle{ADB}=30^\circ$, $\angle{AEB}=2\angle{ADB}$, and $EA=EB$, $D$ must be on the circle with its center at $E$ and its radius as $EB$. Therefore $AE=BE=DE$. And $\triangle{AED}$ is isosceles.
We have $\angle{CED}=\angle{DAE}+\angle{ADE}=10^\circ+10^\circ=20^\circ$. Therefore $\triangle{CDE}$ is isosceles. $CD=DE$. As $DE=BE=AE=AB$, we have $AB=CD$.
