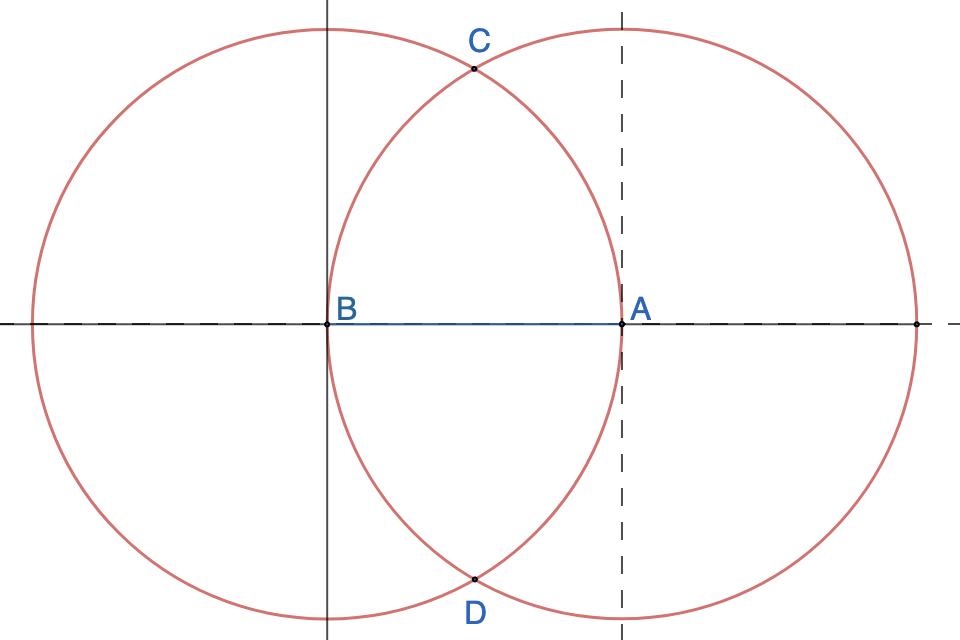
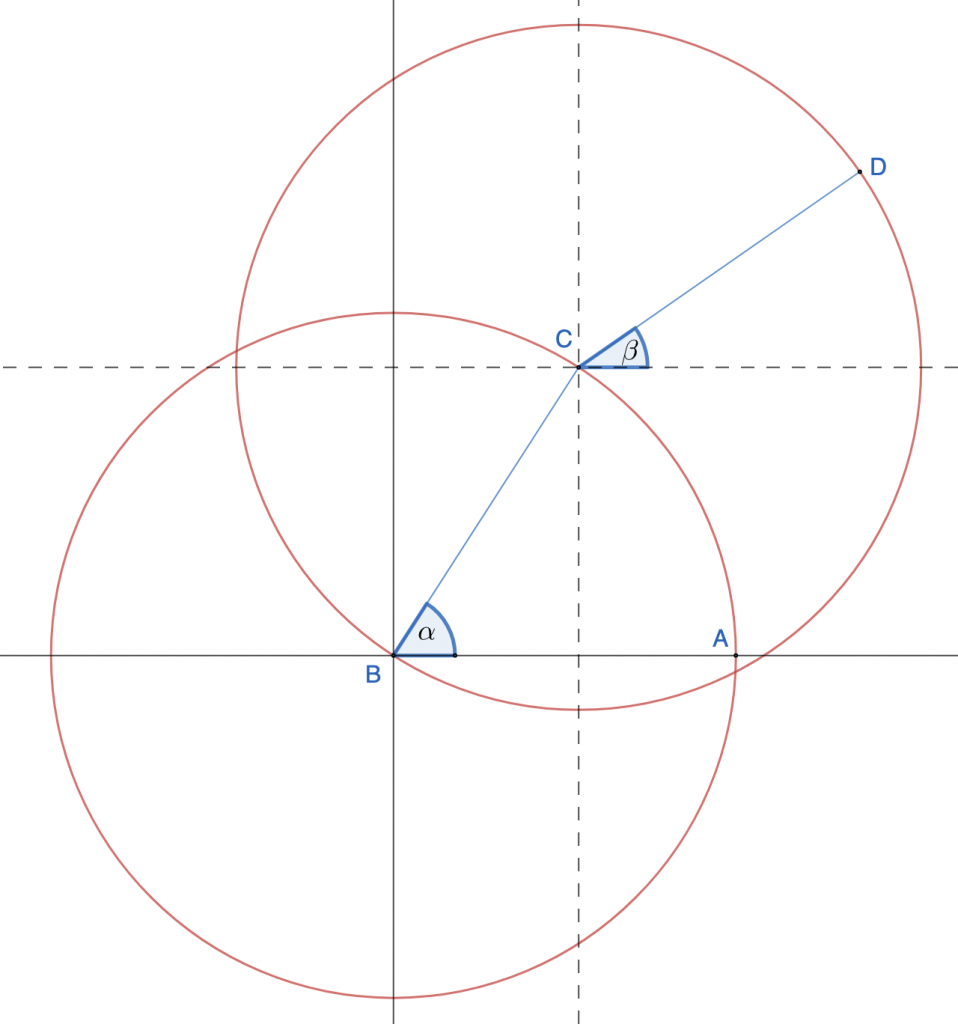
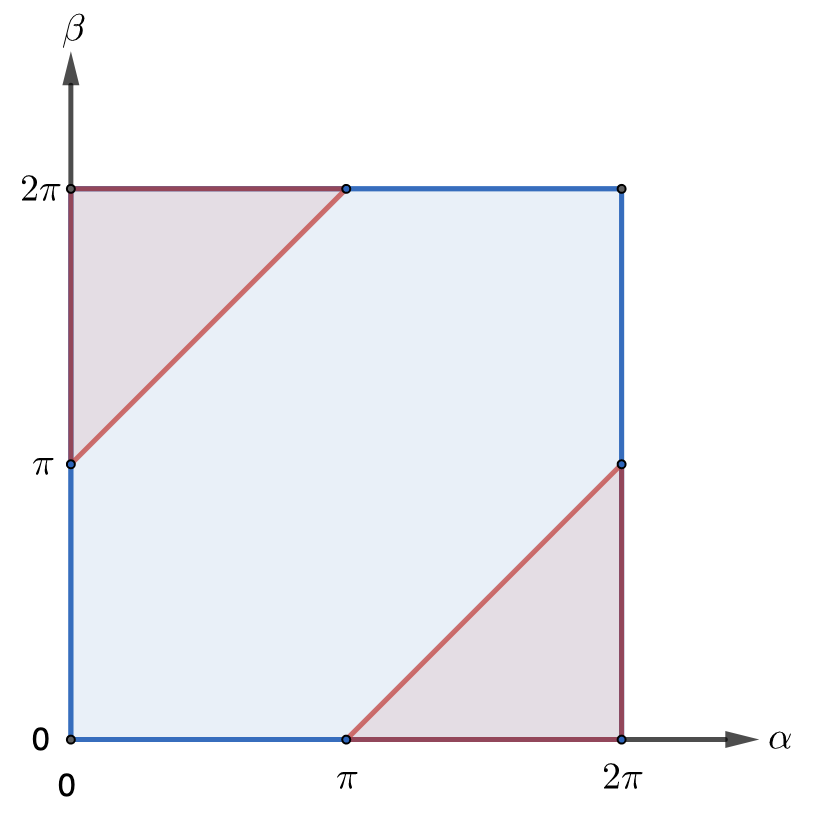
A frog can randomly jump exactly 1 yard away in any random direction constantly. (1) What is the probability that the frog is within 1 yard away from its starting point after 2 jumps? (2) What is the probability that the frog is within 1 yard away from its starting point after 3 jumps? Click here for the solution.
Solution (1): Assume the frog starts at point $A$, and its first jump lands at point $B$:
In order to land the second jump with 1 yard from point $A$, the frog must be land at any point on arc $\overset{\Large\frown}{CAD}$. Since length of arc $\overset{\Large\frown}{CAD}$ is $\dfrac{1}{3}$ of the circumference of the circle centered at point $B$, the probability for the second jump lands within 1 yard from point $A$ is $\boxed{\dfrac{1}{3}}$.
Solution (2): Assume the frog starts at point $A$ with its coordinate as $(1,0)$, and its first jump lands at point $B$ with its coordinate as $(0,0)$, and the second jump lands at point $C$, and the third jump lands at point $D$.
Assume the directional angle along the $x$-axis of the second jump is $\alpha\ (0\le\alpha<2\pi)$, and that of the third jump is $\beta\ (0\le\beta<2\pi)$ . Then, the coordinate of point $D$ would be $(\cos\alpha+\cos\beta,\sin\alpha + \sin\beta)$. Because the distance between $A$ and $D$ must be within 1 yard, therefore $$(\cos\alpha+\cos\beta-1)^2+(\sin\alpha+\sin\beta)^2\le 1 \tag{1}$$ Simplify the above equation, we have $$(\cos\alpha-1)(\cos\beta-1)+\sin\alpha\cdot\sin\beta\le 0 \tag{2}$$ The above inequality can be transformed into the following: $$\sin\dfrac{\alpha}{2}\cdot\sin\dfrac{\beta}{2}\cdot\cos\dfrac{\alpha-\beta}{2}\le 0 \tag{3}$$ Because $0<=\alpha<2\pi$, and $0<=\beta<2\pi$, we have $\sin\dfrac{\alpha}{2}\ge 0$, $\sin\dfrac{\beta}{2}\ge 0$. Therefore $(3)$ can be transformed into the following$$\cos\dfrac{\alpha-\beta}{2}\le 0 \tag{4}$$ Solve the above inequality, we have $$0\le\alpha\lt \pi,\ \alpha+\pi\le\beta\le \pi$$ $$ \pi\le\alpha\lt 2\pi,\ 0\le\beta\le\alpha-\pi$$
As illustrated in the above diagram, the area of the red region, depicted the solutions of $\alpha$ and $\beta$ is $\dfrac{1}{4}$ of the whole square for all possible $\alpha$ and $\beta$ values. Therefore, the probability of the third jump lands within 1 yard of the start point is $\boxed{\dfrac{1}{4}}$.
