An ant makes a sequence of moves on a cube where a move consists of walking from one vertex to an adjacent vertex along an edge of the cube. Initially the ant is at a vertex of the bottom face of the cube and chooses one of the three adjacent vertices to move to as its first move. For all moves after the first move, the ant does not return to its previous vertex, but chooses to move to one of the other two adjacent vertices. All choices are selected at random so that each of the possible moves is equally likely. The probability that after exactly $8$ moves that ant is at a vertex of the top face on the cube is $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
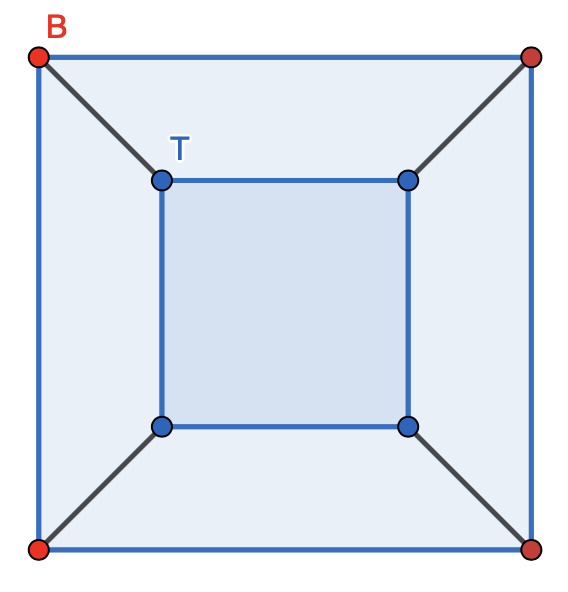
Solution: Let $f(x,y,n)$ donate the probability that the ant eventually stays on the top after moving from vertex $x$ to vertex $y$ with $n$ steps remaining, where $0\le n<8$, $x$ and $y$ are either a vertex on the bottom surface of the cube, donate as $B$, or one on the top surface of the cube, donate as $T$. The probability that after exactly $8$ moves that ant is at a vertex of the top face on the cube is $$p = \dfrac{2}{3}f(B,B,7)+\dfrac{1}{3}f(B,T,7)=\dfrac{2}{3}f(B,B,7)+\dfrac{1}{3}f(T,T,6)$$
$$f(B,B,n)=\dfrac{1}{2}f(B,B,n-1)+\dfrac{1}{2}f(B,T,n-1)=\dfrac{1}{2}f(B,B,n-1)+\dfrac{1}{2}f(T,T,n-2)$$
$$f(T,T,n)=\dfrac{1}{2}f(T,T,n-1)+\dfrac{1}{2}f(T,B,n-1)=\dfrac{1}{2}f(T,T,n-1)+\dfrac{1}{2}f(B,B,n-2)$$
with the following values: $$f(B,B,1)=f(T,T,1)=\dfrac{1}{2}$$ $$f(B,T,1)=f(T,T,0)=1$$ $$f(T,B,1)=f(B,B,0)=0$$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline n&0&1&2&3&4&5&6&7 \\ \hline f(B,B,n)&0&\frac{1}{2}&\frac{3}{4}&\frac{5}{8}&\frac{7}{16}&\frac{13}{32}&\frac{31}{64}&\frac{69}{128} \\ \hline f(T,T,n)&1&\frac{1}{2}&\frac{1}{4}&\frac{3}{8}&\frac{9}{16}&\frac{19}{32}&\frac{33}{64}&\frac{59}{128} \\ \hline \end{array}$$
Therefore, $$p=\dfrac{2}{3}f(B,B,7)+\dfrac{1}{3}f(T,T,6)=\dfrac{2}{3}\cdot\dfrac{69}{128}+\dfrac{1}{3}\cdot\dfrac{33}{64}=\dfrac{17}{32}$$ Therefore $$m+n=\boxed{049}$$
