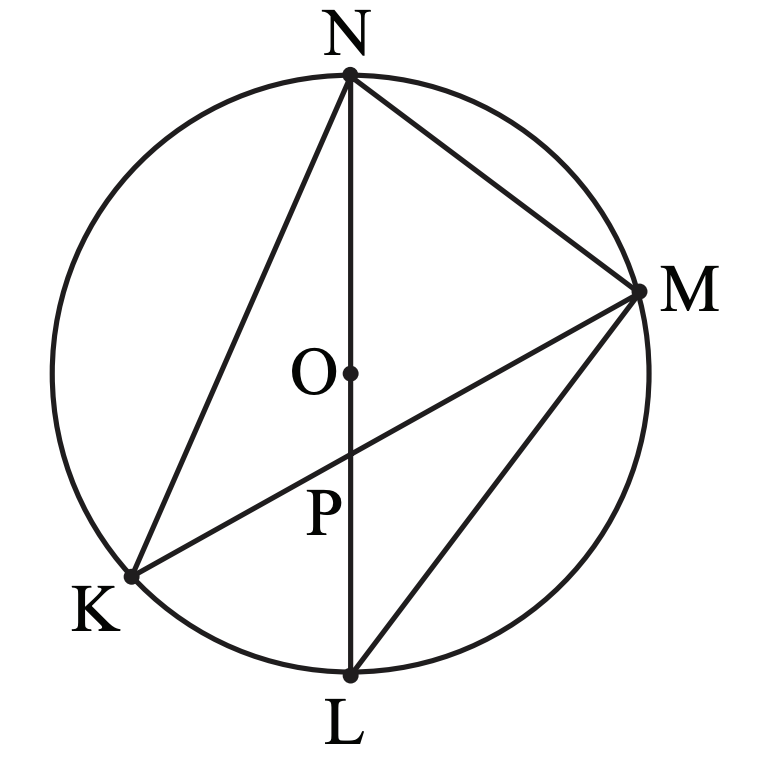
The following is MATHCOUNTS 2012 National Competition Sprint Round Problem 22:
In circle $O$, shown, $OP=2$ units, $PL=8$ units, $PK=9$ units and $NK=18$ units. Points $K$, $P$ and $M$ are collinear, as are points $L$, $P$, $O$ and $N$. What is the length of segment $MN$?
Answer 1: Since $\triangle{KPN}\sim\triangle{LPM}$, we have $$\dfrac{ML}{PL}=\dfrac{NK}{PK}=\dfrac{18}{9}=2$$ $$ML=2\cdot PL=2\cdot 8=16$$Since $\triangle{LMN}$ is a right triangle, therefore $$MN=\sqrt{LN^2-ML^2}=\sqrt{20^2-16^2}=\boxed{12}$$
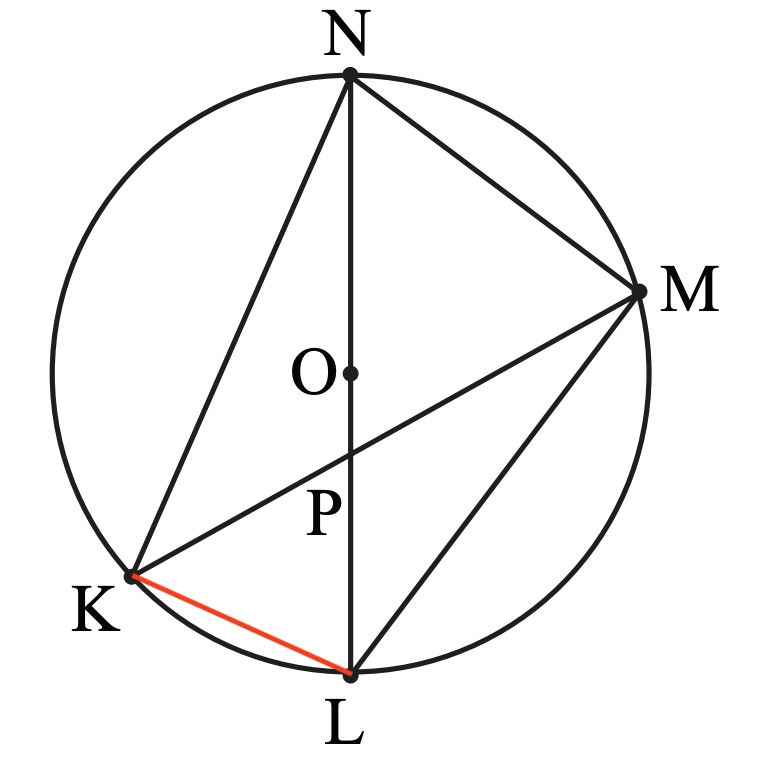
Answer 2: Draw line $KL$, $\triangle{LKN}$ is a right triangle. $$LK=\sqrt{LN^2-NK^2}=\sqrt{20^2-18^2}=2\sqrt{19}$$
Since $\triangle{KPL}\sim\triangle{NPM}$, we have: $$\dfrac{MN}{LK}=\dfrac{PN}{PK}=\dfrac{12}{9}=\dfrac{4}{3}$$ $$MN=\dfrac{4}{3}\cdot LK=\dfrac{4}{3}\cdot 2\sqrt{19}=\boxed{\dfrac{8\sqrt{19}}{3}\approx 11.62}$$
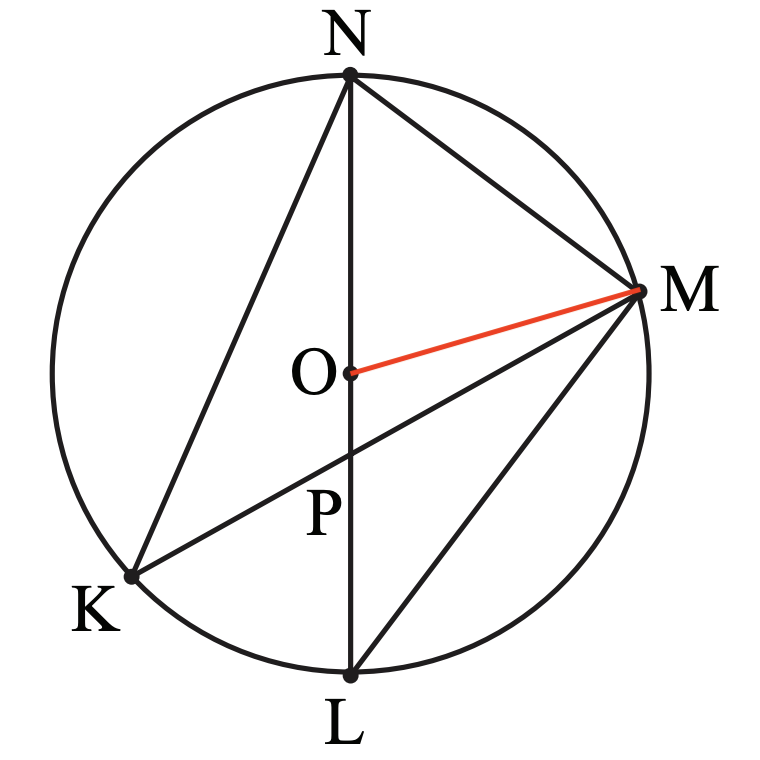
Answer 3: Since $\triangle{KPN}\sim\triangle{LPM}$, we have $$\dfrac{PM}{PL}=\dfrac{PN}{PK}=\dfrac{12}{9}=\dfrac{4}{3}$$ $$PM=\dfrac{4}{3}\cdot PK=\dfrac{4}{3}\cdot 8=\dfrac{32}{3}$$ Draw line $OM$. By the Law of Cosines, we have: $$\cos\angle{MOP}=\dfrac{OP^2+OM^2-PM^2}{2\cdot OP\cdot OM}=\dfrac{2^2+10^2-(\dfrac{32}{3})^2}{2\cdot 2\cdot 10}=-\dfrac{11}{45}$$
Since $\cos\angle{MON}=\cos(180^\circ-\angle{MOP})=-\cos\angle{MOP}=\dfrac{11}{45}$, therefore $$MN=\sqrt{OM^2+ON^2-2\cdot OM\cdot ON\cos\angle{MON}}$$ $$=\sqrt{10^2+10^2-2\cdot 10\cdot 10\cdot\dfrac{11}{45}}=\boxed{\dfrac{4\sqrt{85}}{3}\approx 12.29}$$
Answer 4: Since $\triangle{KPN}\sim\triangle{LPM}$, we have $\dfrac{PM}{PL}=\dfrac{PN}{PK}=\dfrac{12}{9}=\dfrac{4}{3}$. Therefore $$PM=\dfrac{4}{3}\cdot PK=\dfrac{4}{3}\cdot 8=\dfrac{32}{3}$$
By the Law of of Cosines, we have: $$\cos\angle{KPN}=\dfrac{PK^2+PN^2-NK^2}{2\cdot PK\cdot PN}=\dfrac{9^2+12^2-18^2}{2\cdot 9\cdot 12}=-\dfrac{11}{24}$$
Since $\cos\angle{MPN}=\cos(180^\circ-\angle{KPN})=-\cos\angle{KPN}=\dfrac{11}{24}$, therefore $$MN=\sqrt{PN^2+PM^2-2\cdot PN\cdot PM\cdot\cos\angle{MPN}}$$ $$=\sqrt{12^2+(\dfrac{32}{3})^2-2\cdot 12\cdot \dfrac{32}{3}\cdot \dfrac{11}{24}}=\boxed{\dfrac{4\sqrt{79}}{3}\approx 11.85}$$
Reason: The problem was given with incorrect length constraints, as explained by MATHCOUNTS Errata for 2010-2011 through 2014-2015 with the first two answers. In fact, if $NK=18$ units, $PK\neq 9$ units, as shown below:
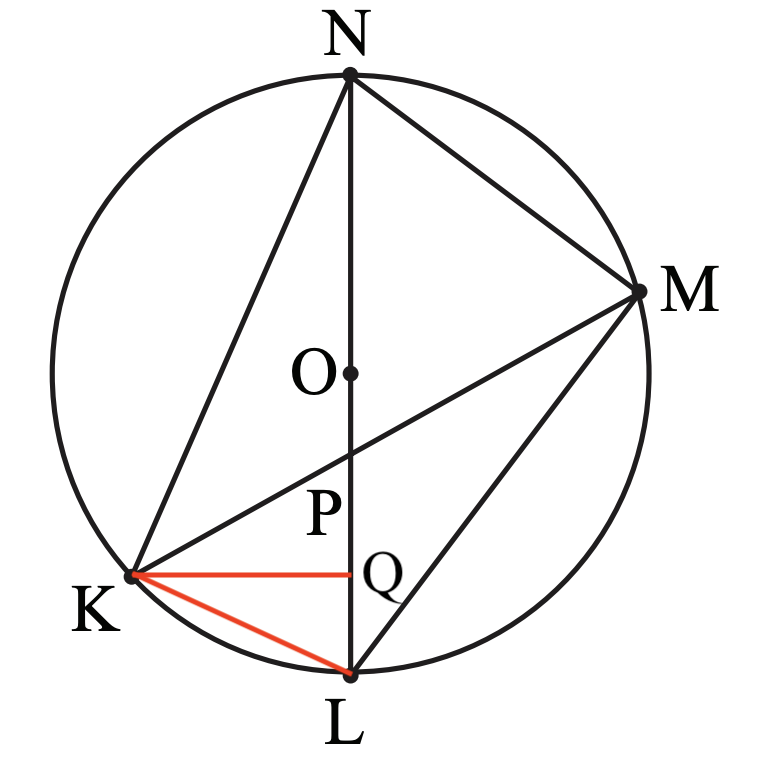
Draw line $KL$ and line $KQ$ perpendicular to line $LN$, intersecting $LN$ at $Q$. Since $\triangle{LKN}$ is a right triangle, we have: $$LK=\sqrt{LN^2-NK^2}=\sqrt{20^2-18^2}=2\sqrt{19}$$ $$KQ=\dfrac{NK\cdot LK}{LN}=\dfrac{18\cdot 2\sqrt{19}}{20}=\dfrac{9\sqrt{19}}{5}$$ $$NQ=\sqrt{NK^2-KQ^2}=\sqrt{18^2-(\dfrac{9\sqrt{19}}{5})^2}=\dfrac{81}{5}$$ $$PQ=NQ-PN=\dfrac{81}{5}-12=\dfrac{21}{5}$$ Therefore $$PK=\sqrt{KQ^2+PQ^2}=\sqrt{(\dfrac{9\sqrt{19}}{5})^2+(\dfrac{21}{5})^2}=\dfrac{6\sqrt{55}}{5}\approx 8.90 \neq 9$$
Because of incorrect length constraints, different calculation methods may lead to different answers $\boxed{🙂}$.
