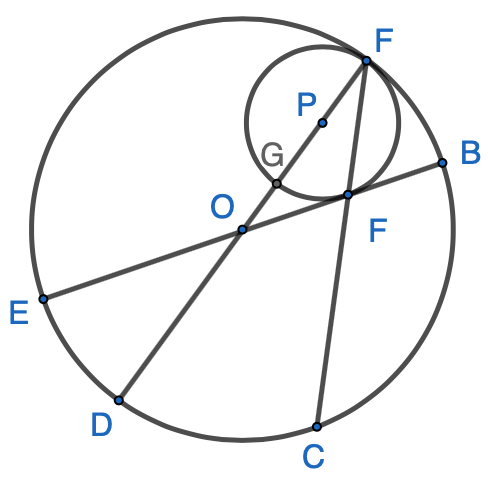
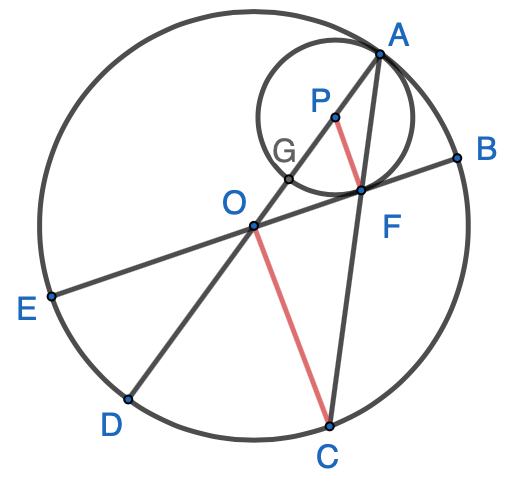
MATHCOUNTS 2016-2017 – 240 Circle $P$ is internally tangent to circle $O$ at $A$, as shown. $\overline{AC}$ and $\overline{BE}$ intersect at $F$, which is also the point of tangency between $\overline{BE}$ and circle $P$. $\overline{AD}$ and $\overline{BE}$ are diameters of circle $O$, and $AG$ is a diameter of circle $P$. If $m\overparen{CD} = 50^\circ$, what is the measure of minor $\overparen{BC}$ ? Click here for the hint