(AIME 2011) In triangle $ABC, AB=\dfrac{20}{11}AC.$ The angle bisector of $\angle A$ intersects $BC$ at point $D$, and point $M$ is the midpoint of $AD$. Let $P$ be the point of intersection of $AC$ and $BM$. Find $\dfrac{CP}{PA}$.
Solution
Without loss of generality, we assume $\triangle ABC$ is a right triangle with legs $AB=20$ and $AC=11$. Constructing the rest of the diagram, we have this:
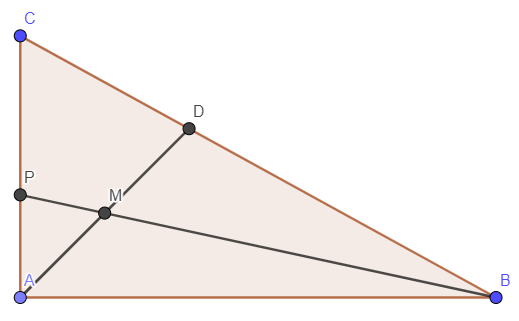
Using the angle bisector theorem, we have $\dfrac{AB}{AC}=\dfrac{CD}{DB}=\dfrac{20}{11}.$ We now can set up mass points, with $\text{mass}(B)=11$ and $\text{mass}(C)=20.$ Then $\text{mass}(D)=\text{mass}(B)+\text{mass}(C)=20+11=31.$ Because $M$ is the midpoint of $AD$, then $\text{mass}(A)=\text{mass}(D)=31.$ Therefore, the ratio $\dfrac{CP}{PA}=\dfrac{\text{mass}(C)}{\text{mass}(A)}=\boxed{\dfrac{20}{13}}.$
