If cans can be placed on top of the one another straight up, how many cylindrical cans $4$ inches in diameter and $6$ inches high can be stored on a shelf $2$ feet wide and $6$ feet long if the shelf is $1$ feet down from the ceiling? Courtney CML Questions Grade 4-6: Problem 362
The standard answer given by CML is $$\dfrac{(2\times 12)\times (6\times 12)}{4\times 4}\times\dfrac{1\times 12}{6}=216$$ That is to store $108$ cans at the bottom, and another $108$ cans on the top.
However, if the cans are stored in the following pattern on the shelf, there will be $$(6\times 10+5\times 10)\times 2=220$$ with $2$ more cans stored on the shelf:
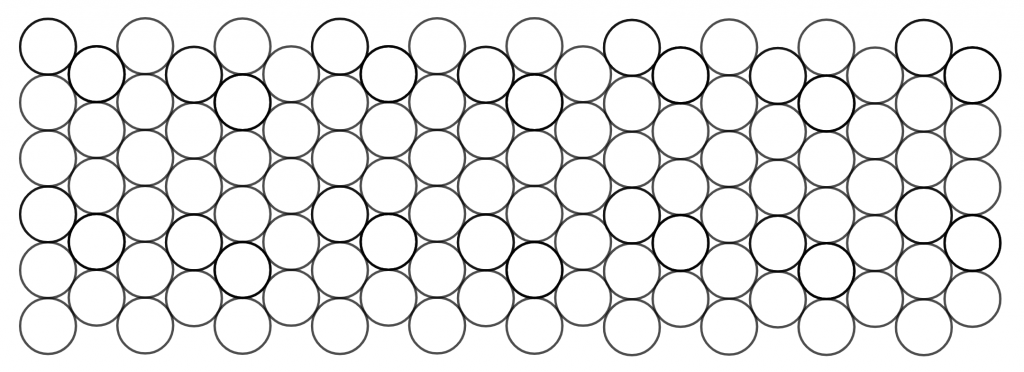
The above packing is more space efficient, as the required length $L$ for placing $n$ columns of cans with diameter as $d$ is $$L=d+(n-1)\cdot\dfrac{\sqrt{3}}{2}\cdot d$$ Given the shelf length as $l$, we have $$n=1+\Big\lfloor \dfrac{2\cdot\sqrt{3}\cdot(l-d)}{3\cdot d}\Big\rfloor$$
If $l=72$ and $d=4$, then $n$=20, with $$L=4+38\sqrt{3}\approx69.816\lt 72$$ leaving more than 2 inches to spare.
If $l=32$ or $l=60$, can you verify that more tighter packing can be done?
