Two dices are thrown simultaneously. The probability that the sum of the two numbers on the top faces of the dices is a prime number is __________.
Suppose $ABCD$ is a regular triangular pyramid, with each face as a unit equilateral triangle. Let S be the midpoint of the edge $AB$ and T the midpoint of the edge of $CD$. The length of $ST$ is _________.
The value of $\dfrac{(2^3-1)(3^3-1)(4^3-1)…(100^3-1)}{(2^3+1)(3^3+1)(4^3+1)…(100^3+1)}$ is __________.
If $x^2+\dfrac{1}{x^2}=47$, the value of $\sqrt{x}+\dfrac{1}{\sqrt{x}}$ is __________.
4 shoes are randomly selected from 4 pair of shoes in different colors. The probability of 4 shoes containing at least one pair in same color selected is __________.
For all real number $x$, $f(x+1)=\dfrac{1+f(x)}{1-f(x)}$. If $f(2)=2$, then $f(2020)=$ __________.
Positive integer $k$, $m$, and $n$ satisfy the equation $\dfrac{k}{m}+\dfrac{m}{4n}=\dfrac{1}{6}$. The smallest value of $m$ is __________.
The value of $100^2-99^2+98^2-97^2+96^2-95^2+…+4^2-3^2+2^2-1^2$ is __________.
Let $ABCD$ be a quadrilateral. Let $E$,$F$,$G$, and $H$ be the midpoints of sides $AB$,$BC$,$CD$, and $DA$, respectively. The ratio of the area of the quadrilateral $EFGH$ to that of the quadrilateral $ABCD$ is __________.
A convex quadrilateral is formed by randomly selecting four distinct points on the circumference of a circle. The probability of the quadrilateral is inside half of the circle is __________.
The total number of ways to distribute 6 distinguish gifts to 3 children with each child having at least one gift is __________.
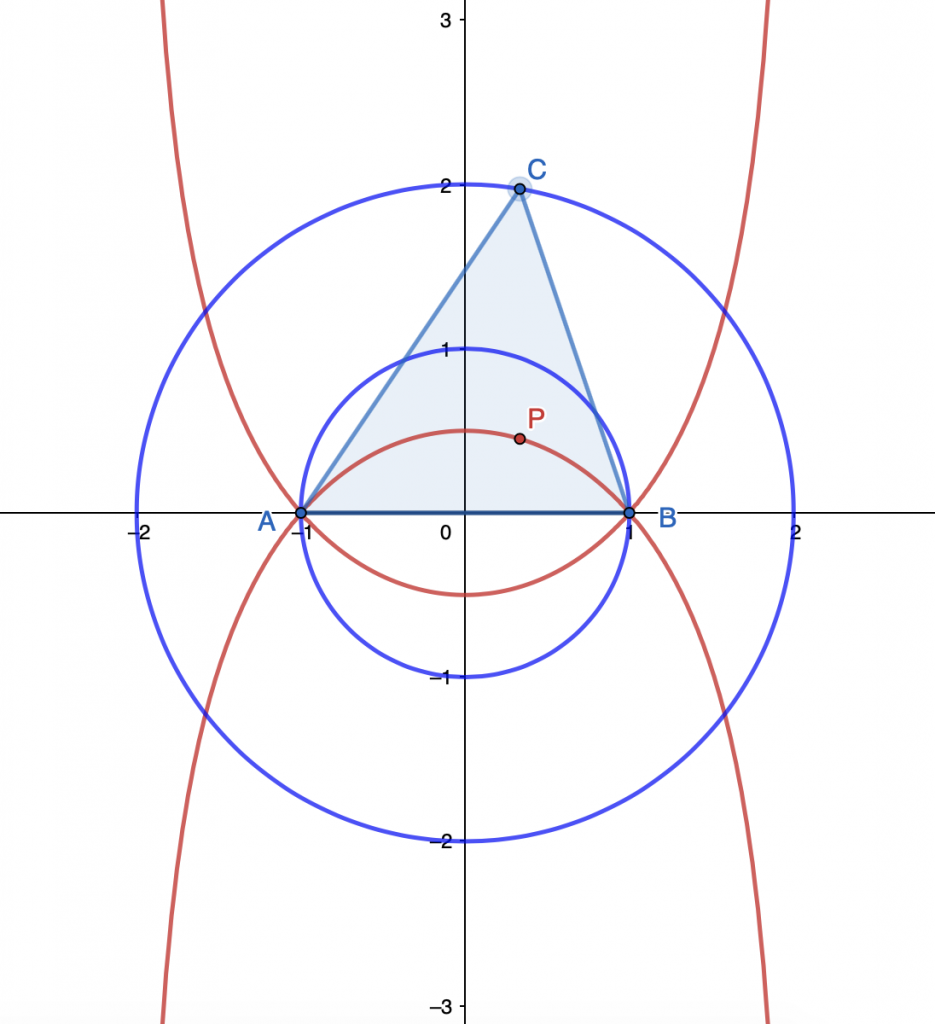
Let $P$ be a point inside an equilateral $\triangle{ABC}$, with $PA = 4$, $PB = 3$, and $PC = 5$. The side length of $\triangle{ABC}$ is __________.
The number of factors of $2^5\times 3^6\times 5^2$ are perfect squares is __________.
There are 4 oranges, 5 apples and 6 mangoes in a basket. The number of ways that a person make a selection of fruits among the fruits in the basket is __________.
5 adults and 3 kids are seated in a round table. The number of ways that all 3 kids are not sitting together is __________.
In a chess competition involving some men and women, every player needs to play exactly one game with every other player. It was found that in 45 games, both the players were women and in 190 games, both players were men. The number of games in which one person was a man and other person was a woman is __________.
In $\triangle{ABC}$, point $D$, $E$, $F$, $G$, and $H$ are on side $BC$, point $I$, $J$, $K$ are on side $AC$. Draw line $AD$, $AE$, $AF$, $AG$, $AH$, $BI$, $BJ$, and $BK$. The number of unique triangles formed by various lines are __________.
Answer: 134
One corner of a cube is cut off by a plane. The minimum number of corners in the remaining part of the cube is __________.
The smallest natural number with $12$ factors is ________.
The remainder of 6666666666….6666666 divided by 7 is __________ with 6 repeated 2020 times.
Adam, Bob, Carl, Dave and Ed are playing chess against each other. Each pair play one match. After awhile, if Adam has played 4 matches, Bob 3 matches, Carl 2 matches, and Dave 1 match, the number of matches Ed has played is __________.
A truck is moving from City A to City B. If the truck speed is increased 20%, the truck can arrive at City B 1 hour earlier. After the truck has traveled 120 miles at its normal speed, its speeds was increased 25% and arrived at City B 40 minutes earlier. The distance between City A and City B is ________ miles.
Answer: 270
Solution: Set up some equations that will help us solve for the variables \(t\) for time, \(r\) for the normal truck speed, and \(d\) for the distance between A and B. Using the first information given, we can set up two equations: $$d=rt$$ $$t-1=\frac{d}{1.2r}$$ With the last equation, here is where it gets tricky.
40 minutes is equivalent to $\frac{2}{3}$ hours, so our left side of the equation is $t-\frac{2}{3}$. The right side is more difficult. The first part of the trip is 120 miles long and at the speed of $r$, so the time taken there is $\frac{120}{r}$. The second part is $d-120$ miles long and is at the speed of $1.25r$, giving the expression $\frac{d-120}{1.25r}$. Therefore, we get the equation $$t-\frac{2}{3}=\frac{120}{r}+\frac{d-120}{1.25r}$$ Combining all three equations together, we get $$d=rt$$ $$t-1=\frac{d}{1.2r}$$ $$t-\frac{2}{3}=\frac{120}{r}+\frac{d-120}{1.25r}$$
First, taking the first 2 equations together, we can get $d=1.2rt-1.2r$. Substituting, we obtain the equation $rt=1.2rt-1.2r$. Therefore, $1.2r=0.2rt$, which simplifies to $6r=rt$. Dividing by $r$ gives $t=6$.
Substituting all $t$’s for 6’s and all $d$’s with $rt$’s, we get $$6-\frac{2}{3}=\frac{120}{r}+\frac{6r-120}{1.25r}$$ This becomes $$\frac{16}{3}=\frac{120+24r}{5r}$$ Solving the proportion gives $r=45$. Since $d=rt$, and $t=6$, substituting $r$ gives $d=(45)(6)=\boxed{270}$.
In parallelogram $ABCD$, $DE$ is perpendicular to $AB$. intersecting $AB$ at point $E$ and diagonal $AC$ at point $F$. If $AD:FC=1:2$, then $\angle{CAB}:\angle{CAD}=$__________.
An isosceles trapezoid is tangent to a unit circle on all its sides. If the area of the trapezoid is 4, the perimeter if the trapezoid is __________.
In $\triangle{ABC}$, $\angle{ACB}=90^\circ$, $AC=8$, $BC=15$, $D$ is a point on $AB$. If $CD=AC$, then $AD=$__________.
In trapezoid $ABCD$, $AB \parallel CD$. Diagonal $AC$ and $BD$ intersect at point $E$. If the area of $\triangle{AEB}$ is $m^2$, and that of $\triangle{CED}$ is $n^2$, then, the area of trapeziod $ABCD$ is ________.
In trapezoid $ABCD$, $AB \parallel CD$. Diagonal $AC$ and $BD$ intersect at point $O$. Line $EF$ pass thru $O$ and $EF \parallel AB$, intersecting $AD$ at point $E$, $BC$ at point $F$. If $AB=a$, $CD=d$, then $EF=$ ________.
In $\triangle{ABC}$, $\overline{AB}=1$. Point $D$ is on $\overline{AB}$ and point $E$ is on $\overline{AC}$ such that $\overline{DE} \parallel \overline{BC}$. If $\dfrac{[ADE]}{[BCD]}=k$, then what is $\dfrac{[ADE]}{[ABC]}$ in terms of $k$?
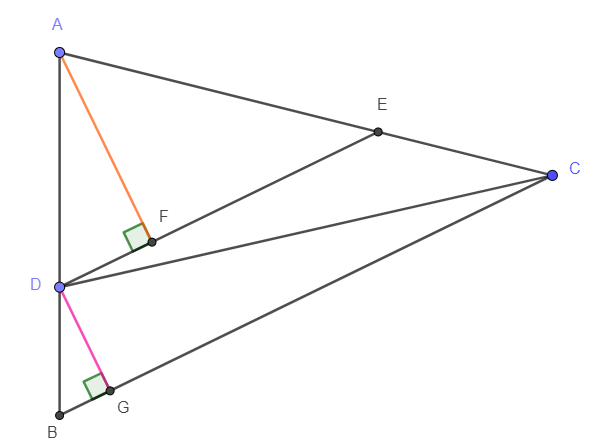
First, draw the altitudes for triangles $ADE$ and $BCD$, each intersecting $DE$ and $BC$ at points $F$ and $G$, respectively. Let $x=AD$. Therefore, $BD=1-x$. We can use similar triangles to get $\dfrac{1-x}{x}=\dfrac{AF}{DG}$ and $\dfrac{1}{x}=\dfrac{BC}{DE}$. Using the triangles’ area properties, we get $DE\cdot AF = k\cdot BC \cdot DG$.
With our similarity properties discussed above, we can simplify the area ratio to a ratio between $AF$ and $DG$: $$AF=\dfrac{k}{x} DG$$ Plugging this back into the equation, we get $\dfrac{1-x}{x}=\dfrac{x}{k}$. Cross multiplying obtains $x^2=k-kx$, creating a quadratic $x^2+kx-k=0$. Solving for the roots, we get $$x=\dfrac{-k \pm \sqrt{k^2+4k}}{2}$$ Noticing that $\sqrt{k^2+nk}\geq k$, we can determine that $$x = \dfrac{-k + \sqrt{k^2+4k}}{2}$$ Therefore, $$\dfrac{[ADE]}{[ABC]} = x^2 = \boxed{\dfrac{2k+k^2-k\sqrt{k^2+4k}}{2}}$$